
分析 (1)观察已知等式,归纳总结得到一般性规律,写出即可;
(2)根据得出的规律将原式化简,合并即可得到结果.
解答 解:(1)根据题意得:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$(n≥1,且n为正整数);
故答案为:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$(n≥1,且n为正整数);
(2)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)=($\sqrt{2016}$-1)($\sqrt{2016}$+1)=2016-1=2015.
点评 此题考查了分母有理化,弄清题中的规律是解本题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
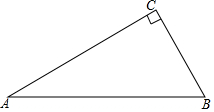 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
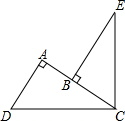 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.
如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com