
【题目】已知,如图,在ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.

【答案】(1)详见解析;(2)4.
【解析】
(1)先证明四边形ABEF是平行四边形,再证明邻边相等即可证明.
(2)由菱形的对角线平分对角和等边三角形的判定推知△ABE是等边三角形,则AE=AB.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EBF=∠AFB,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠ABF=∠AFB,
∴AB=AF,
∵BO⊥AE,
∴∠AOB=∠EOB=90°,
∵BO=BO,
在△BOA和△BOE中,
 ,
,
∴△BOA≌△BOE(ASA),
∴AB=BE,
∴BE=AF,BE∥AF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形;
(2)解:菱形ABEF的周长为16,∠BEF=120°,
∴BE=AB=4,∠AEB=60°,
∴△ABE是等边三角形,则AE=AB=4.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() ,求
,求![]() 的度数. (提示:作
的度数. (提示:作![]() ).
).
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,求
,求![]() 与
与![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点![]() 在射线
在射线![]() 上运动,请你直接写出
上运动,请你直接写出![]() 与
与![]() 、
、![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,则线段AF的长的最小值 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)解方程:|3x-2|-4=0.
(2)解关于x的方程:|x-2|=b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为_____千米.
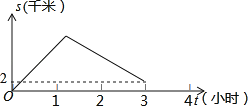
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.方程x2-4x+2=0无实数根;
B.两条对角线互相垂直且相等的四边形是正方形
C.甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是 ![]()
D.若 ![]() 是反比例函数,则k的值为2或-1。
是反比例函数,则k的值为2或-1。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:﹣12+(π﹣3.14)0﹣(﹣![]() )﹣2+
)﹣2+![]() ;
;
(2)先化简,再求值:[(2x+y)(2x﹣y)+(x+y)2﹣2(2x2﹣xy)]÷(﹣![]() x),其中x、y满足
x),其中x、y满足![]() +(y+4)2=0.
+(y+4)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你完成下面的证明:
已知:如图,∠GFB+∠B=180°,∠1=∠3,
求证:FC∥ED.
证明:∵∠GFB+∠B=180°
∴FG∥BC( )
∴∠3= ( ),
又∵∠1=∠3(已知)
∴∠1= (等量代换)
∴FC∥ED( )
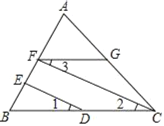
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是
是![]() 的直角三角形,
的直角三角形,![]() 的中点分别是点
的中点分别是点![]() 点
点![]() ,动点
,动点![]() 从点
从点![]() 出发,按箭头方向通过
出发,按箭头方向通过![]() 到
到![]() ;以
;以![]() 的速度运动,设
的速度运动,设![]() 点从
点从![]() 开始运动的距离为
开始运动的距离为![]() ,
,![]() 的面积为
的面积为![]() 试回答以下问题:
试回答以下问题:
(1)![]() 点从
点从![]() 出发到
出发到![]() 停止,写出
停止,写出![]() 与
与![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围.
的取值范围.
(2)求出![]() 点从
点从![]() 出发后几秒时,
出发后几秒时,![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com