
����Ŀ�����������ƿ���ִ�2013����ÿ���ȫ��������ѧ������������ϲ���������μ����������飨������ѧ��ÿ��ֻ��ѡһ�������������������ݻ��Ƴ�ͼ1��ͼ2����ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ����������⣺
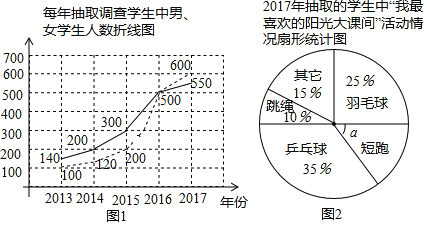
��1���� �����ȡ�ĵ����������٣��� �����ȡ�ĵ���������������Ů��������ȣ�
��2����ͼ2����������������ͼ����ռ��Բ�Ľ����Ķ�����
��3��2017���ȡ��ѧ���У�ϲ����ë��Ͷ��ܵ�ѧ�����ж����ˣ�
��4�����2017��ȫ�й���3.4������ѧ���������������2017��ϲ��ƹ�������ë�������˶��Ĵ�Լ�ж����ˣ�
���𰸡���1��2013��2016����2��54������3��460�ˣ���4��20400��
��������
��1����ͼ�е����ݽ����жϼ��ɣ�
��2���������������������ͼ����ռ�İٷֱ�Ϊ15%�������õ�����360���15%��54����
��3������2017���ȡ��ѧ�����������ɵõ�ϲ����ë��Ͷ��ܵ�ѧ��������
��4������ϲ��ƹ�������ë�������˶��İٷֱȣ����ɹ�������2017��ϲ��ƹ�������ë�������˶���������
�⣺��1����ͼ�ɵã�2013���ȡ�ĵ����������٣�2016���ȡ�ĵ���������������Ů��������ȣ�
�ʴ�Ϊ��2013��2016��
��2��1��35%��10%��15%��25%��15%��
������360���15%��54����
��3��2017���ȡ��ѧ���У�ϲ����ë��Ͷ��ܵ�ѧ�����У�600+550������25%+15%����460���ˣ���
��4������2017��ϲ��ƹ�������ë�������˶��Ĵ�Լ��34000����25%+35%����20400���ˣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����̲ij��֣���ͼ�ǻ�ʦ����꼶�ϲ���ѧ�̲ĵ�78ҳ�IJ�������.
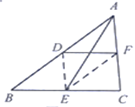
��1 ��֤�������ε�һ����λ����������ϵ�������ƽ��.
��֪����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() .
.
��֤��![]() ��
��![]() ����ƽ��.
����ƽ��.
֤��������![]() ��
��![]() .
.
����ݽ̲���ʾ�����ͼ�٣�д�������Ľ������.
������Ӧ�ã���ͼ�ڣ�����ͼ�ٵ�![]() ��
��![]() ���ֱ���
���ֱ���![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() .
.
��1����![]() �����
�����![]() ��
��![]() ֮��ľ���.
֮��ľ���.
��2�����ı���![]() �����Ϊ2����
�����Ϊ2����![]() �����Ϊ______.
�����Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�
��x�ύ�ڵ�![]() ����
����![]() ����y�ύ�ڵ�C���ҹ���
����y�ύ�ڵ�C���ҹ���![]() ����P��Q��������
����P��Q��������![]() �ϵĶ��㣮
�ϵĶ��㣮
(1)�������ߵĽ���ʽ��
(2)����P��ֱ��OD�·�ʱ����![]() ��������ֵ��
��������ֵ��
(3)ֱ��OQ���߶�BC�ཻ�ڵ�E����![]() ��
��![]() ����ʱ�����Q�����꣮
����ʱ�����Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
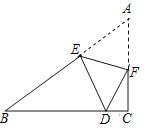
����Ŀ����ͼ��Rt��ABC�У���ACB=90����AC=3��BC=4����E��F�ֱ��ڱ�AB��AC�ϣ�����AEF��ֱ��EF�۵���ʹ��A�Ķ�Ӧ��Dǡ�����ڱ�BC�ϣ�����BDE��ֱ�������Σ���CF�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��
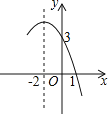
�ٵ�y��0ʱ��x��ȡֵ��Χ��______��
�ڷ���ax2+bx+c=3�Ľ���______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��ax2+bx��3��ֱ��y��x+3���ڵ�A��m��0���͵�B��2��n������y�ύ�ڵ�C��
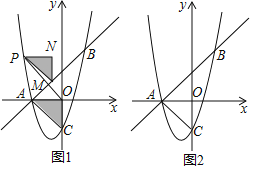
��1����m��n��ֵ�������ߵĽ���ʽ��
��2����ͼ1�У�����AOCƽ�ƣ�ʼ�ձ��ֵ�A�Ķ�Ӧ��P���������ϣ���C��O�Ķ�Ӧ��ֱ�ΪM��N������OP������Mǡ����ֱ��y��x+3�ϣ����߶�OP�ij��ȣ�
��3����ͼ2�������������Ƿ���ڵ�Q�������C�غϣ���ʹ��QAB����ABC�������ȣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ�����.Ϊ�����л����㴫ͳ�Ļ���ij��ѧ��������֯��һ��ȫУ2000��ѧ���μӵ���������д������.Ϊ�˽Ȿ�δ����ijɼ���ѧУ�����������ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
�ɼ�x���֣������� | Ƶ�����ˣ� | Ƶ�� |
50��x<60 | 10 | 0.05 |
60��x<70 | 30 | 0.15 |
70��x<80 | 40 | 0.2 |
80��x<90 | m | 0.35 |
90��x<100 | 50 | n |
Ƶ���ֲ�ֱ��ͼ

������������Ϣ���ش��������⣺
��1��m=________��n=________��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ��������________�����Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ�������ȣ�������Ƹ�У�μӱ��α�����2000��ѧ���гɼ����������ȵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�BC��10cm��DC��6cm����E��F�ֱ�Ϊ��AB��BC�ϵ��������㣬E�ӵ�A������ÿ��5cm���ٶ���B�˶���F�ӵ�B������ÿ��3cm���ٶ���C�˶������˶�ʱ��Ϊt�룮����AFD����AED����t��ֵ_____��
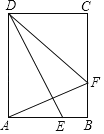
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=-x2+bx+c�Ķ���ΪC���Գ���Ϊֱ��x=1���Ҿ�����A��3��-1������y�ύ�ڵ�B��
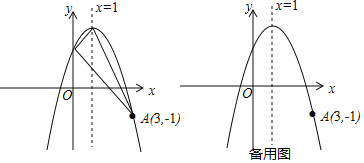
��1���������ߵĽ���ʽ��
��2���ж���ABC����״����˵�����ɣ�
��3��������A��ֱ�߽��������ڵ�P����x���ڵ�Q����S��OPA=2S��OQA���������P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com