
����Ŀ��Ϊ�˽��Уѧ����5G�ƶ�ͨ�������������Ը������У��ѧ���������ȡ��1000�˽��е��飬�����Ǵ�ѧ���û��������ͳ�Ʊ��ʹ�ѧ��Ը��Ϊ5G�ײͶ�֧���ķ������ͳ��ͼ�����磬���������û���Ը��Ϊ5G�ײͶ�֧��10Ԫ������ռ�������������û���50%����
�û����� | ���� |
A�����������û���Ŀǰ������Ϊ5G�û��� | 260�� |
B�����ڸ����û���һ���ڽ�����Ϊ5G�û��� | 540�� |
C�������û���һ��������Ϊ5G�û��� | 200�� |
�����ƶ��У����������ǣ� ��

A.���������û��У�Ը��Ϊ5G�ײͶ�֧��10Ԫ��20Ԫ��30Ԫ���������εݼ�
B.�����û��У�Ը��Ϊ5G�ײͶ�֧��20Ԫ���������
C.Ը��Ϊ5G�ײͶ�֧��10Ԫ���û��У����ڸ����û��������
D.Ը��Ϊ5G�ײͶ�֧��20Ԫ���û��У������û��������
���𰸡�D
��������
�ֱ��������������û������ڸ����û��������û���֧��10Ԫ��20Ԫ��30Ԫ�������ٷ������ɣ�
���������û���֧��10Ԫ����![]() ��֧��20Ԫ����
��֧��20Ԫ����![]() ��֧��30Ԫ����
��֧��30Ԫ����![]()
���ڸ����û���֧��10Ԫ����![]() ��֧��20Ԫ����
��֧��20Ԫ����![]() ��֧��30Ԫ����
��֧��30Ԫ����![]()
�����û���֧��10Ԫ����![]() ��֧��20Ԫ����
��֧��20Ԫ����![]() ��֧��30Ԫ����
��֧��30Ԫ����![]()
A�����������û��У�Ը��Ϊ5G�ײͶ�֧��10Ԫ��20Ԫ��30Ԫ���������εݼ���˵����ȷ���ʴ�ѡ�������
B�������û��У�Ը��Ϊ5G�ײͶ�֧��20Ԫ��������࣬˵����ȷ���ʴ�ѡ�������
C��Ը��Ϊ5G�ײͶ�֧��10Ԫ���û��У����ڸ����û�������࣬˵����ȷ���ʴ�ѡ�������
D��Ը��Ϊ5G�ײͶ�֧��20Ԫ���û��У������û�������࣬˵����ȷ��ӦΪ���ڸ����û���࣬�ʴ�ѡ���������
��ѡ��D��


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB��26��P��AB��(�����A��B�غ�)����һ�㣬��C��DΪ��O�ϵ����㣬����APD����BPC����ơ�CPDΪֱ��AB�ġ������ǡ���
(1)����BPC����DPC��60�㣬���CPD��ֱ��AB�ġ������ǡ��𣿲�˵�����ɣ�
(2)��![]() �ij�Ϊ
�ij�Ϊ![]() ���������ǡ���CPD�Ķ�����
���������ǡ���CPD�Ķ�����
(3)��ֱ��AB�ġ������ǡ�Ϊ120�㣬�ҡ�PCD���ܳ�Ϊ24+13![]() ��ֱ��д��AP�ij���
��ֱ��д��AP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
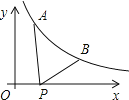
����Ŀ����ͼ��ʾ����֪A��![]() ��y1����B(2,y2)Ϊ����������
��y1����B(2,y2)Ϊ����������![]() ͼ���ϵ����㣬����P(x��0)��x���������˶������߶�AP���߶�BP֮��ﵽ���ʱ����P�������ǣ� ��
ͼ���ϵ����㣬����P(x��0)��x���������˶������߶�AP���߶�BP֮��ﵽ���ʱ����P�������ǣ� ��
A. (![]() ��0) B. (1,0) C. (
��0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c��ͼ����ͼ��ʾ������˵����ȷ���ǣ� ��
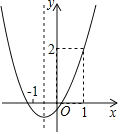
A.abc��0B.a��b+c��2
C.4ac��b2��0D.��x����1ʱ��y��x���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
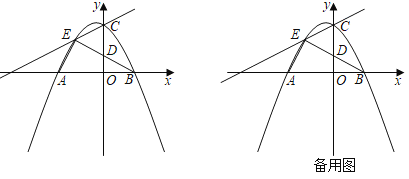
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx+c��ͼ����x�ύ��A����3��0����B��2��0�����㣬��y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
��2����E��m��2����ֱ��AC�Ϸ�����������һ�㣬����EA��EB��EC��EB��y�ύ��D��
�ٵ�F��x����һ���㣬����EF������A��E��FΪ��������������BOD����ʱ������߶�EF�ij���
�ڵ�GΪy�������������һ�㣬����G��ֱ��CE�Ĵ��ߣ�����ΪH������GCH����EBA����ֱ��д����H�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
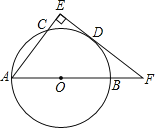
����Ŀ����ͼ��ABΪ��O��ֱ����ACΪ�ң���DΪ![]() �е㣬����D��DE��ֱ��AC������ΪE����AB���ӳ����ڵ�F
�е㣬����D��DE��ֱ��AC������ΪE����AB���ӳ����ڵ�F
��1����֤��EF�ǡ�O�����ߣ�
��2����EF��4��sin��F��![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��a��2b��2��4ab����������y=x2+4x+10�ϣ����A���������߶Գ���ĶԳƵ�����Ϊ��������
A. ����3��7�� B. ����1��7�� C. ����4��10�� D. ��0��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
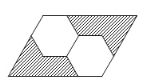
����Ŀ����ͼ��ʾ��ƽ���ı�����������ȫ�ȵ��������Σ�����Ӱ���ֵ������Ϊ![]() ��ƽ���ı��ε������Ϊ
��ƽ���ı��ε������Ϊ![]() ,��
,��![]() ��ֵΪ____��
��ֵΪ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
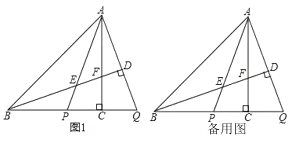
����Ŀ����ͼ���ڵ���ֱ�ǡ�ABC�У���ACB=90��P���߶�BC�ϣ��ӳ�BC����Q��ʹ��CQ=CP������AP��AQ������B��BD��AQ�ڵ�D����AP�ڵ�E����AC�ڵ�F��K���߶�AD�ϵ�һ������(���A��D���غ�)������K��GN��AP�ڵ�H����AB�ڵ�G����AC�ڵ�M����FD���ӳ����ڵ�N��
(1)�����ⲹȫͼ1��
(2)��֤��NM=NF��
(3)��AM=CP���õ�ʽ��ʾ�߶�AE��GN��BN֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com