
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(![]() +1)EH;③
+1)EH;③![]() =
=![]() . 其中正确的是( )
. 其中正确的是( )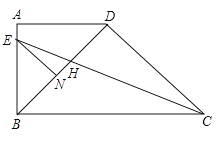
A.①②
B.②③
C.①③
D.①②③
【答案】B
【解析】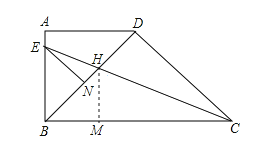 ①如图,过H作HM⊥BC于M,
①如图,过H作HM⊥BC于M,
∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=![]() x=BE,
x=BE,
∴EN=x,
∴CD=BD=DH+BH=(![]() +1)x,
+1)x,
即![]() =
=![]() +1,
+1,
∵EN∥DC,
∴△DCH∽△NEH,
∴![]() =
=![]() =
=![]() +1,即CH=(
+1,即CH=(![]() +1)EH,正确;
+1)EH,正确;
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而![]() =
=![]() ,
,
∴![]() =
=![]() , 正确;
, 正确;
所以正确的只有②③.
故选B.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握直角梯形(一腰垂直于底的梯形是直角梯形)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) 
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ABC=90°,BD是∠ABC的平分线,DE⊥AB于点E , DF⊥BC于点F . 求证:四边形DEBF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )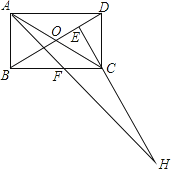
A.②③
B.③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.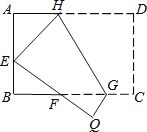
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com