
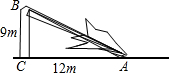
 如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米.
如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
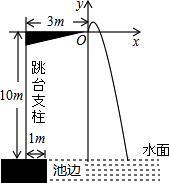 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米.
如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com