
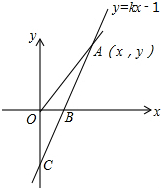
 ��ͼ��ֱ��y=kx-1��x�ᡢy��ֱ���B��C���㣬��OC=2OB��
��ͼ��ֱ��y=kx-1��x�ᡢy��ֱ���B��C���㣬��OC=2OB������ ��1����x=0����ֱ�ߵĽ���ʽ�õ�y=-1���ʴ�OC=1���Ӷ��õ���B������Ϊ��$\frac{1}{2}$��0��������B���������y=kx-1�����k=2��
��2����ͼ1��ʾ������A��AD��x�ᣬ����ΪD�������ֱ�ߵĽ���ʽy=2x-1��Ȼ�����������ε������ʽ�ɵõ�S=$\frac{1}{2}x-\frac{1}{4}$��x$��\frac{1}{2}$����
��3������S=$\frac{1}{4}$���x=1�����ǿ����A��1��1����
�ڿɸ���AP=AO��PA=PO��OP=OA���������ͼ��⼴�ɣ�
��� �⣺��1���߽�x=0����ã�y=-1��
���C��������0��-1����
��OC=1��
��OC=2OB��
��OB=$\frac{1}{2}$��
���B��������$\frac{1}{2}$��0����
����B���������y=kx-1�ã�$\frac{1}{2}k-1=0$��
��ã�k=2��
��2����ͼ1��ʾ������A��AD��x�ᣬ����ΪD��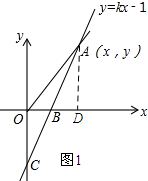
��k=2��
��ֱ�ߵĽ���ʽΪy=2x-1��
��${S}_{��AOB}=\frac{1}{2}OB•AD$=$\frac{1}{2}��\frac{1}{2}����2x-1��$=$\frac{1}{2}x-\frac{1}{4}$��
��S=$\frac{1}{2}x-\frac{1}{4}$��x$��\frac{1}{2}$����
��3������S=$\frac{1}{4}$�ã�$\frac{1}{2}x-\frac{1}{4}$=$\frac{1}{4}$��
��ã�x=1��
��x=1����y=2x-1�ã�y=1��
���A��������1��1����
�൱��A���˶�����1��1����ʱ����AOB�����Ϊ$\frac{1}{4}$��
�ڡߵ�A������Ϊ��1��1����
��OA=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$��
��AP=AOʱ����ͼ2��ʾ������A��AB��y�ᣬ����ΪB��
��AP=AO��AB��OP��
��OB=PB��
���P��������0��2����
��PA=POʱ����ͼ3��ʾ��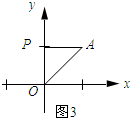
��PO=PA=1��
���P��������0��1����
��ͼ4��ʾ����OP=OAʱ��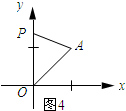
��OP=OA=$\sqrt{2}$��
���P��������0��$\sqrt{2}$����
��ͼ5��ʾ����OP=OAʱ��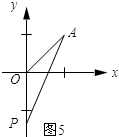
��OP=OA=$\sqrt{2}$��
���P��������0��-$\sqrt{2}$����
������������P��������0��2����0��1����0��$\sqrt{2}$����0��-$\sqrt{2}$����
���� ������Ҫ�������һ�κ������ۺ�Ӧ�á��������ҪӦ���˴���ϵ���������Ľ���ʽ�����������ε��ж�������AP=AO��PA=PO��OP=OA�������������ͼ���ǽ���Ĺؼ���


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����1=��2�����1�͡�2�ǶԶ��� | |
| B�� | ��ǵĶԶ���Ҳ����� | |
| C�� | �Զ��Ƕ������ | |
| D�� | �����1�͡�2�й����Ķ��㣮���1�͡�2�ǶԶ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
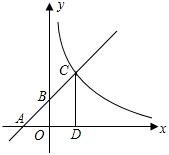 ��ͼ����֪һ�κ���y=kx+b��ͼ����x�ᣬy��ֱ��ཻ��A��B���㣬���뷴���к���y=$\frac{m}{x}$�ڵ�һ����ͼ���ڵ�C��CD��ֱ��x�ᣬ����ΪD�����OA=OB=OD=1����
��ͼ����֪һ�κ���y=kx+b��ͼ����x�ᣬy��ֱ��ཻ��A��B���㣬���뷴���к���y=$\frac{m}{x}$�ڵ�һ����ͼ���ڵ�C��CD��ֱ��x�ᣬ����ΪD�����OA=OB=OD=1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
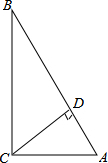 �ڡ�ABC�У���C=90�㣬�����ֱ�������Σ�
�ڡ�ABC�У���C=90�㣬�����ֱ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���������ϣ���A��ʾ����Ϊ10����B��ʾ����Ϊ13����Mɥʾ������-20����
��֪����ͼ���������ϣ���A��ʾ����Ϊ10����B��ʾ����Ϊ13����Mɥʾ������-20�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1-��-$\frac{1}{2}$��=-1$\frac{1}{2}$ | B�� | |a-3|=a-3 | C�� | ��-7.3��+6.4=-0.9 | D�� | 8+|-8|=0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com