【题目】如图，在四边形ABCD中，∠A=120°，∠C=80°．将△BMN沿着MN翻折，得到△FMN．若MF∥AD，FN∥DC，则∠F的度数为（ ）
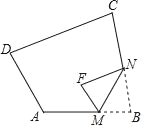
A. 70° B. 80° C. 90° D. 100°
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案科目：初中数学 来源： 题型：
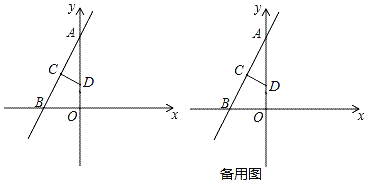
【题目】如图，在平面直角坐标系中，A（0，8），B（﹣4，0），线段AB的垂直平分线CD分别交AB、OA于点C、D，其中点D的坐标为（0，3）．
（1）求直线AB的解析式；
（2）求线段CD的长；
（3）点E为y轴上一个动点，当△CDE为等腰三角形时，求E点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，则CE的长为 ．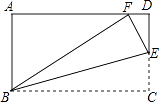 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列推理过程，将空白部分补充完整．
（1）如图1，∠ABC=∠A1B1C1，BD，B1D1分别是∠ABC，∠A1B1C1的角平分线，对∠DBC=∠D1B1C1进行说理．
理由：因为BD，B1D1分别是∠ABC，∠A1B1C1的角平分线
所以∠DBC= ，∠D1B1C1= （角平分线的定义）
又因为∠ABC=∠A1B1C1
所以
∠ABC=∠A1B1C1
所以∠DBC=∠D1B1C1（ ）
（2）如图2，EF∥AD，∠1=∠2，∠B=40°，求∠CDG的度数．
因为EF∥AD，
所以∠2= （ ）
又因为∠1=∠2 （已知）
所以∠1= （等量代换）
所以AB∥GD（ ）
所以∠B= （ ）
因为∠B=40°（已知）
所以∠CDG= （等量代换）
（3）下面是“积的乘方的法则“的推导过程，在括号里写出每一步的依据．
因为（ab）n=
（ ）
=
（ ）
=anbn（ ）
所以（ab）n=anbn．
查看答案和解析>>
科目：初中数学 来源： 题型：
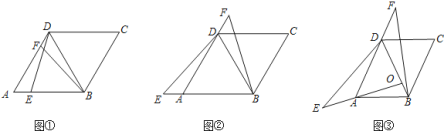
【题目】感知：如图
，在菱形ABCD中，
，点E、F分别在边AB、AD上
若
，易知
≌
．
探究：如图
，在菱形ABCD中，，点E、F分别在BA、AD的延长线上若，与是否全等？如果全等，请证明；如果不全等，请说明理由．
拓展：如图
，在ABCD中，
，点O是AD边的垂直平分线与BD的交点，点E、F分别在OA、AD的延长线上若，
，
，求
的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数y= 
的图象上．若点B在反比例函数y= 
的图象上，则k的值为 ．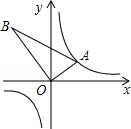 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD的对角线AC、BD的长分别为10厘米、6厘米，且AC与BD互相垂直，顺次连接四边形ABCD四边的中点E、F、G、H得四边形EFGH，则四边形EFGH的面积为_____平方厘米．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某车间有技术工人85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配成一套，问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套？并求出加工了多少套？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
