
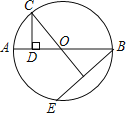
【题目】如图,在⊙O中,AB是直径,弦BE的垂直平分线交⊙O于点C,CD⊥AB于D,AD=1,BE=6,则BD的长为__.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 与
与![]() ,下列判断不正确的是( )
,下列判断不正确的是( )
A.若方程![]() 有两个实数根,则方程
有两个实数根,则方程![]() 也有两个实数根;
也有两个实数根;
B.如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是
是![]() 的一个根;
的一个根;
C.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1;
有一个根相等,那么这个根是1;
D.如果方程![]() 与
与![]() 有一个根相等,那么这个根是1或-1.
有一个根相等,那么这个根是1或-1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
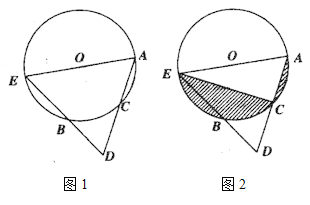
【题目】如图1,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图2,连接CE,⊙O的半径为5,AC长为4,求阴影部分面积之和.(保留![]() 与根号) .
与根号) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD和正方形AEFG中,点B在边AG上,点D在线段EA的延长线上,连接BE.
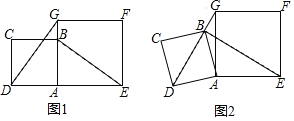
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,使点B恰好落在线段DG上.
①求证:DG⊥BE;
②若AB=2,AG=3,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D时线段AB上一动点,连接BE.
填空:①![]() 的值为 ; ②∠DBE的度数为 .
的值为 ; ②∠DBE的度数为 .

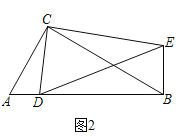
(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由;
的值及∠DBE的度数,并说明理由;
(3)拓展延伸
如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型工厂9月份生产的A、B两种产品数量分别为200件和100件,A、B两种产品出厂单价之比为2:1,由于订单的增加,工厂提高了A、B两种产品的生产数量和出厂单价,10月份A产品生产数量的增长率和A产品出厂单价的增长率相等,B产品生产数量的增长率是A产品生产数量的增长率的一半,B产品出厂单价的增长率是A产品出厂单价的增长率的2倍.设B产品生产数量的增长率为x(x>0).
(1)用含有x的代数式填表(不需化简):
9月份生产数量 | 生产数量的增长率 | 10月份生产数量 | |
产品A | 200 |
|
|
产品B | 100 | x |
|
(2)若9月份两种产品出厂单价的和为90元,10月份该工厂的总收入增加了4.4x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com