
”¾ĢāÄæ”æĶź³ÉĻĀĆęµÄÖ¤Ć÷¹ż³Ģ£ŗ
ČēĶ¼£¬AB”ĪCD£¬AD”ĪBC£¬BEĘ½·Ö”ĻABC£¬DFĘ½·Ö”ĻADC£®
ĒóÖ¤£ŗBE”ĪDF£®

Ö¤Ć÷£ŗ”ßAB”ĪCD£¬£ØŅŃÖŖ£©
”ą”ĻABC+”ĻC£½180”ć£®£Ø”” ”” £©
ÓÖ”ßAD”ĪBC£¬£ØŅŃÖŖ£©
”ą”” ””+”ĻC£½180”ć£®£Ø”” ”” £©
”ą”ĻABC£½”ĻADC£®£Ø”” ”” £©
”ßBEĘ½·Ö”ĻABC£¬£ØŅŃÖŖ£©
”ą”Ļ1£½![]() ”ĻABC£®£Ø”” ”” £©
”ĻABC£®£Ø”” ”” £©
Ķ¬Ąķ£¬”Ļ2£½![]() ”ĻADC£®
”ĻADC£®
”ą”” ””£½”Ļ2£®
”ßAD”ĪBC£¬£ØŅŃÖŖ£©
”ą”Ļ2£½”Ļ3£®£Ø”” ”” £©
”ą”Ļ1£½”Ļ3£¬
”ąBE”ĪDF£®£Ø”” ”” £©
”¾“š°ø”æĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£»”ĻADC£»Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£»Ķ¬½ĒµÄ²¹½ĒĻąµČ£»½ĒµÄĘ½·ÖĻߵĶØŅ壻”Ļ1£»Į½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£»Ķ¬Ī»½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£®
”¾½āĪö”æ
ĻČÓÉĘ½ŠŠĻߵĊŌÖŹÖŖ”ĻABC+”ĻC=”ĻADC+”ĻC=180”ćÖŖ”ĻABC=”ĻADC£¬øł¾Ż½ĒĘ½·ÖĻߵĶØŅåÖ¤”Ļ1=”Ļ2£¬½įŗĻAD”ĪBCµĆ”Ļ2=”Ļ3£¬øł¾ŻĘ½ŠŠĻߵĊŌÖŹµĆ”Ļ1=”Ļ3£¬“Ó¶ųµĆÖ¤£®
Ö¤Ć÷£ŗ”ßAB”ĪCD£¬£ØŅŃÖŖ£©
”ą”ĻABC+”ĻC=180”ć£®£ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£©
ÓÖ”ßAD”ĪBC£¬£ØŅŃÖŖ£©
”ą”ĻADC+”ĻC=180”ć£®£ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£©
”ą”ĻABC=”ĻADC£®£ØĶ¬½ĒµÄ²¹½ĒĻąµČ£©
”ßBEĘ½·Ö”ĻABC£¬£ØŅŃÖŖ£©
”ą”Ļ1=![]() ”ĻABC£®£Ø½ĒµÄĘ½·ÖĻߵĶØŅ壩
”ĻABC£®£Ø½ĒµÄĘ½·ÖĻߵĶØŅ壩
Ķ¬Ąķ£¬”Ļ2=![]() ”ĻADC£®
”ĻADC£®
”ą”Ļ1=”Ļ2£®
”ßAD”ĪBC£¬£ØŅŃÖŖ£©
”ą”Ļ2=”Ļ3£®£ØĮ½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£©
”ą”Ļ1=”Ļ3£¬
”ąBE”ĪDF£®£ØĶ¬Ī»½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£©
¹Ź“š°øĪŖ£ŗĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£»”ĻADC£»Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹£»Ķ¬½ĒµÄ²¹½ĒĻąµČ£»½ĒµÄĘ½·ÖĻߵĶØŅ壻”Ļ1£»Į½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£»Ķ¬Ī»½ĒĻąµČ£¬Į½Ö±ĻßĘ½ŠŠ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ŃĖÄÕÅŠĪד“óŠ”ĶźČ«ĻąĶ¬µÄŠ”Õż·½ŠĪæØʬ(ČēĶ¼1)²»ÖŲµžµŲ·ÅŌŚŅ»øöµ×ĆęĪŖ³¤·½ŠĪ(³¤ĪŖmcm£¬æķĪŖncm)µÄŗŠ×ӵĵײæ(ČēĶ¼2)£¬ŗŠ×Óµ×ĆęĪ“±»æØʬø²øĒµÄ²æ·ÖÓĆŅõÓ°±ķŹ¾.ŌņĶ¼2ÖŠĮ½æéŅõÓ°²æ·ÖµÄÖܳ¤ŗĶŹĒ£Ø £©

A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDµÄ±ß³¤ŹĒ16£¬µćEŌŚ±ßABÉĻ£¬AE=3£¬µćFŹĒ±ßBCÉĻ²»ÓėµćB£¬CÖŲŗĻµÄŅ»øö¶Æµć£¬°Ń”÷EBFŃŲEFÕŪµž£¬µćBĀäŌŚB”䓦£®Čō”÷CDB”äĒ”ĪŖµČŃüČż½ĒŠĪ£¬ŌņDB”äµÄ³¤ĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖAµć×ų±źĪŖ(5£¬0)£¬Ö±Ļßy£½kx+b(b£¾0)ÓėyÖį½»ÓŚµćB£¬”ĻBCA£½60”ć£¬Į¬½ÓAB£¬”Ļ¦Į£½105”ć£¬ŌņÖ±Ļßy£½kx+bµÄ±ķ“ļŹ½ĪŖ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā·½³Ģ£Ø×飩
£Ø1£©2£Øx©1£©3+16=0£®
£Ø2£©![]() £»
£»
£Ø3£© £®
£®
£Ø4£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
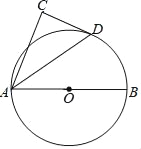
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬DĪŖ”ŃOÉĻŅ»µć£¬ŅŌADĪŖŠ±±ß×÷”÷ADC£¬Ź¹”ĻC=90”ć£¬”ĻCAD=”ĻDAB
£Ø1£©ĒóÖ¤£ŗDCŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ČōAB=9£¬AD=6£¬ĒóDCµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCDÖŠ£¬EĪŖBCµÄÖŠµć£¬Į¬½ÓAE²¢ŃÓ³¤½»DCµÄŃÓ³¤ĻßÓŚµćF.
(1)ĒóÖ¤£ŗAB£½CF£»
(2)µ±BCÓėAFĀś×ćŹ²Ć“ŹżĮæ¹ŲĻµŹ±£¬ĖıߊĪABFCŹĒ¾ŲŠĪ£¬²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¢Å Ģ½¾æ·¢ĻÖ
¢Ł ![]() _________£»
_________£»
¢Ś ![]() _________£»
_________£»
¢Ū ![]() _________£»
_________£»
¢Ü _________________£»
” ”
¢Ę ¹ęĀÉĢįĮ¶
Š“³öµŚnøöµČŹ½£ØÓĆŗ¬ÓŠ×ÖÄø![]() µÄŹ½×Ó±ķŹ¾£©£®
µÄŹ½×Ó±ķŹ¾£©£®
¢Ē ĪŹĢā½ā¾ö
¢Ł ![]() _______£»
_______£»
¢Ś Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ±ß³¤ĪŖ 2 µÄÕż·½ŠĪ ABCD ÖŠ£¬µć P ”¢Q ·Ö±šŹĒ±ß AB ”¢ BC ÉĻµÄĮ½øö¶Æµć£ØÓėµć A ”¢B ”¢C ²»ÖŲŗĻ£©ĒŅŹ¼ÖÕ±£³Ö BP BQ, AQ QE £¬QE ½»Õż·½ŠĪĶā½ĒĘ½·ÖĻßCE ÓŚµć E £¬ AE ½»CD ÓŚµć F £¬Į¬½į PQ ”£
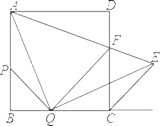
£Ø1£©ĒóÖ¤£ŗ APQ ”Õ QCE £»
£Ø2£©ĒóQAE µÄ¶ČŹż£»
£Ø3£©Éč BQ x £¬µ± x ĪŖŗĪÖµŹ±£¬ QF CE £¬²¢Ēó³ö“ĖŹ±AQF µÄĆ껿”£
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com