
 дкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌОиаЮOABCЕФЮЛжУШчЭМЫљЪОЃЌЕуAЃЌCЕФзјБъЗжБ№ЮЊЃЈ10ЃЌ0ЃЉЃЌЃЈ0ЃЌ8ЃЉЃЎЕуPЪЧyжсе§АыжсЩЯЕФвЛИіЖЏЕуЃЌНЋЁїOAPбиAPЗелЕУЕНЁїOЁфAPЃЌжБЯпBCгыжБЯпOЁфPНЛгкЕуEЃЌгыжБЯпOA'НЛгкЕуFЃЎ
дкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌОиаЮOABCЕФЮЛжУШчЭМЫљЪОЃЌЕуAЃЌCЕФзјБъЗжБ№ЮЊЃЈ10ЃЌ0ЃЉЃЌЃЈ0ЃЌ8ЃЉЃЎЕуPЪЧyжсе§АыжсЩЯЕФвЛИіЖЏЕуЃЌНЋЁїOAPбиAPЗелЕУЕНЁїOЁфAPЃЌжБЯпBCгыжБЯпOЁфPНЛгкЕуEЃЌгыжБЯпOA'НЛгкЕуFЃЎЗжЮі ЃЈ1ЃЉСЌНгOЁфOЃЌзїOЁфGЁЭOAгкЕуGЃЌИљОнAO=AOЁфЃЌЁЯOЁфAO=2ЁЯOPA=60ЁуЃЌМДПЩЕУГіЁїOЁфAOЪЧЕШБпШ§НЧаЮЃЌдйНсКЯЕуAЕФзјБъМДПЩЕУГіЕуOЁфЕФзјБъЃЛ
ЃЈ2ЃЉЩшжБЯпOЁфAЕФНтЮіЪНЮЊy=kx+bЃЌИљОнЙДЙЩЖЈРэПЩЕУГіBOЁфЕФГЄЖШЃЌдйИљОнOЁфдкЯпЖЮBCЩЯКЭOЁфдкCBбгГЄЯпЩЯЗжСНжжЧщПіПМТЧЃЌгЩДЫМДПЩЕУГіЕуOЁфЕФзјБъЃЌНсКЯЕуAOЁфЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЕУГіжБЯпOЁфAЕФНтЮіЪНЃЛ
ЃЈ3ЃЉМйЩшДцдкЃЌЩшЕуPЃЈ0ЃЌmЃЉЃЌИљОнЕуOЁфдкжБЯпBCЕФЩЯЯТСНВрРДЗжРрЬжТлЃЎИљОнЦНааЯпЕФаджЪевГіЯрЕШЕФНЧДгЖјЕУГіСНШ§НЧаЮЯрЫЦЃЌдйИљОнЯрЫЦШ§НЧаЮЕФаджЪЃЈЛђЕШНЧЕФШ§НЧКЏЪ§жЕЯрЕШЃЉевГіБпгыБпжЎМфЕФЙиЯЕЃЌгЩДЫМДПЩСаГіЙигкmЕФЗНГЬЃЌНтЗНГЬМДПЩЕУГіНсТлЃЎ
НтД№ 25ЃЎНтЃКЃЈ1ЃЉСЌНгOЁфOЃЌзїOЁфGЁЭOAгкЕуGЃЌШчЭМ1ЫљЪОЃЎ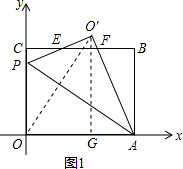
ЁЯOЁфAO=2ЁЯOPA=60ЁуЃЌAO=AOЁфЃЌ
ЁрЁїOЁфAOЪЧЕШБпШ§НЧаЮЃЌ
ЁпЕуAЕФзјБъЮЊЃЈ10ЃЌ0ЃЉЃЌ
ЁрOA=10ЃЌOG=$\frac{1}{2}$OA=5ЃЌOЁфG=$\frac{\sqrt{3}}{2}$OA=5$\sqrt{3}$ЃЌ
ЁрЕуOЁфЕФзјБъЮЊЃЈ5ЃЌ5$\sqrt{3}$ЃЉЃЎ
ЃЈ2ЃЉЩшжБЯпOЁфAЕФНтЮіЪНЮЊy=kx+bЃЎ
дкRtЁїABOЁфжаЃЌAOЁф=10ЃЌAB=8ЃЌ
ЁрBOЁфЈT6ЃЌ
ЂйЕБOЁфдкЯпЖЮBCЩЯЪБЃЌCOЁф=10-6=4ЃЌ
ЁрЕуOЁфЕФзјБъЮЊЃЈ4ЃЌ8ЃЉЃЌ
дђга$\left\{\begin{array}{l}{0=10k+b}\\{8=4k+b}\end{array}\right.$ЃЌНтЕУЃК$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{40}{3}}\end{array}\right.$ЃЌ
ЁрДЫЪБжБЯпOЁфAЕФНтЮіЪНЮЊy=-$\frac{4}{3}$x+$\frac{40}{3}$ЃЛ
ЂкЕБOЁфдкCBбгГЄЯпЩЯЪБЃЌCOЁф=10+6=16ЃЌ
ЁрЕуOЁфЕФзјБъЮЊЃЈ16ЃЌ8ЃЉЃЌ
дђга$\left\{\begin{array}{l}{0=10k+b}\\{8=16k+b}\end{array}\right.$ЃЌНтЕУЃК$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{40}{3}}\end{array}\right.$
ЁрДЫЪБжБЯпOЁфAЕФНтЮіЪНЮЊy=$\frac{4}{3}$x-$\frac{40}{3}$ЃЎ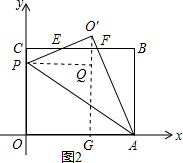
ЃЈ3ЃЉМйЩшДцдкЃЌгЩЕуOЁфЕФЮЛжУВЛЭЌЗжСНжжЧщПіЃК
ЂйЕБЕуOЁфдкBCЕФЩЯЗНЪБЃЌЩшЕуPЃЈ0ЃЌmЃЉЃЌЙ§ЕуOЁфзїOЁфGЁЭOAгкЕуGЃЌЙ§ЕуPзїPQЁЭOЁфGгкЕуQЃЌШчЭМ2ЫљЪОЃЎ
ЁпOP=CFЃЌ
ЁрBF=BC-CF=10-mЃЌ
ЁпЕуCЃЈ0ЃЌ8ЃЉЃЌ
ЁрAB=OC=8ЃЎ
дкRtЁїABFжаЃЌAB=8ЃЌBF=10-mЃЌ
ЁрAF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{64+ЃЈ10-mЃЉ^{2}}$ЃЎ
ЁпOЁфGЁЭxжсЃЌABЁЭOAЃЌ
ЁрOЁфGЁЮABЃЌ
ЁрЁїOЁфGAЁзЁїABFЃЌ
Ёр$\frac{OЁфG}{AB}=\frac{AG}{BF}=\frac{AOЁф}{AF}$ЃЌ
ЁрOЁфG=$\frac{80}{\sqrt{64+ЃЈ10-mЃЉ^{2}}}$ЃЌAG=$\frac{10•ЃЈ10-mЃЉ}{\sqrt{64+ЃЈ10-mЃЉ^{2}}}$ЃЌ
ЁрOЁфQ=OЁфG-OP=$\frac{80}{\sqrt{64+ЃЈ10-mЃЉ^{2}}}$-mЃЌPQ=OA-AG=10-$\frac{10•ЃЈ10-mЃЉ}{\sqrt{64+ЃЈ10-mЃЉ^{2}}}$ЃЎ
ЁпЁЯPOЁфQ+ЁЯOЁфPQ=90ЁуЃЌЁЯPOЁфQ+ЁЯAOЁфG=90ЁуЃЌ
ЁрЁЯOЁфPQ=ЁЯAOЁфG=ЁЯFABЃЌ
Ёр$\frac{PQ}{AB}=\frac{POЁф}{AF}$ЃЌ
ЁрPQ=$\frac{8m}{\sqrt{64+ЃЈ10-mЃЉ^{2}}}$=10-$\frac{10•ЃЈ10-mЃЉ}{\sqrt{64+ЃЈ10-mЃЉ^{2}}}$ЃЌ
НтЕУЃКm1=$\frac{20}{3}$ЃЌm2=10ЃЌ
ОМьбщm1=$\frac{20}{3}$ЪЧЗжЪНЗНГЬЕФНтЃЌ
ДЫЪБЕуPЕФзјБъЮЊЃЈ0ЃЌ$\frac{20}{3}$ЃЉЃЛ
ЂкЕБЕуOЁфдкBCЕФЯТЗНЪБЃЌЩшAFгыyжсЕФНЛЕуЮЊMЃЌШчЭМ3ЫљЪОЃЎ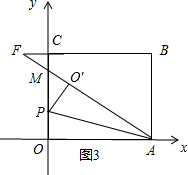
ЩшЕуPЃЈ0ЃЌmЃЉЃЌдђCF=OP=mЃЌ
BF=10+mЃЌAB=8ЃЌOA=10ЃЌAF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{64+ЃЈ10+mЃЉ^{2}}$ЃЎ
ЁпBCЁЮAOЃЌ
ЁрЁЯAFB=ЁЯMAOЃЌ
Ёр$\frac{AB}{OM}=\frac{BF}{OA}$ЃЌ
ЁрOM=$\frac{80}{10+m}$ЃЌ
ЁрPM=OM-OP=$\frac{80}{10+m}$-mЃЌ
ЁпЁЯMPOЁфгыЁЯAMOЛЅгрЃЌ
ЁрЁЯMPOЁф=ЁЯAFBЃЌ
Ёр$\frac{POЁф}{PM}=\frac{BF}{AF}$ЃЌМД$\frac{m}{\frac{80}{10+m}-m}=\frac{10+m}{\sqrt{64+ЃЈ10+mЃЉ^{2}}}$ЃЌ
НтЕУЃКm3=$\frac{20}{7}$ЃЌm4=-10ЃЈЩсШЅЃЉЃЌ
ОМьбщm3=$\frac{20}{7}$ЪЧЗжЪНЗНГЬЕФНтЃЌ
ДЫЪБЕуPЕФзјБъЮЊЃЈ0ЃЌ$\frac{20}{7}$ЃЉЃЎ
злЩЯПЩжЊЃКЕБЕуPдкОиаЮOABCБпOCЕФдЫЖЏЙ§ГЬжаЃЌДцдкФГвЛЪБПЬЃЌЪЙЕУЯпЖЮCFгыЯпЖЮOPЕФГЄЖШЯрЕШЃЌЕуPЕФзјБъЮЊЃЈ0ЃЌ$\frac{20}{3}$ЃЉЛђЃЈ0ЃЌ$\frac{20}{7}$ЃЉЃЎ
ЕуЦР БОЬтПМВщСЫЕШБпШ§НЧаЮЕФХаЖЈМАаджЪЁЂД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЁЂЦНааЯпЕФаджЪвдМАЯрЫЦШ§НЧаЮЕФХаЖЈМАаджЪЃЌНтЬтЕФЙиМќЪЧЃКЃЈ1ЃЉЕУГіЁїOЁфAOЪЧЕШБпШ§НЧаЮЃЛЃЈ2ЃЉЗжСНжжЧщПіЧѓГіЕуOЁфЕФзјБъЃЛЃЈ3ЃЉЗжЧщПіевГіЙигкmЕФЗНГЬЃЎБОЬтЪєгкжаЕЕЬтЃЌФбЖШВЛДѓЃЌгШЦфдкНтОіЃЈ3ЃЉЪБЃЌЭљЭљжЛЛсПМТЧЕНЕквЛжжЧщПіЖјЭќМЧЕкЖўжжЧщПідьГЩЪЇЗжЃЌвђДЫдкШеГЃСЗЯАжавЊзЂвтХрбјПМТЧЮЪЬтЕФШЋУцадЃЎ


 аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ
аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\sqrt{16}$=ЁР4 | BЃЎ | $\sqrt{16}$=-4 | CЃЎ | $ЁР\sqrt{16}=ЁР4$ | DЃЎ | $\sqrt{-16}$=-4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌЗЩЛњЗЩааИпЖШЮЊ2000mЃЌЗЩаадБПДЕиЦНУцжИЛгЬЈAЕФИЉНЧЮЊІСЃЌдђЗЩЛњгыжИЛгЬЈAЕФОрРыЮЊЃЈЕЅЮЛЃКmЃЉЃЈЁЁЁЁЃЉ
ШчЭМЃЌЗЩЛњЗЩааИпЖШЮЊ2000mЃЌЗЩаадБПДЕиЦНУцжИЛгЬЈAЕФИЉНЧЮЊІСЃЌдђЗЩЛњгыжИЛгЬЈAЕФОрРыЮЊЃЈЕЅЮЛЃКmЃЉЃЈЁЁЁЁЃЉ| AЃЎ | $\frac{2000}{sinІС}$ | BЃЎ | 2000sinІС | CЃЎ | 2000cosІС | DЃЎ | $\frac{2000}{tanІС}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -1 | BЃЎ | 1 | CЃЎ | 3 | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌЦНааЫФБпаЮABCDЕФжмГЄЪЧ26cmЃЌЖдНЧЯпACгыBDНЛгкЕуOЃЌACЁЭABЃЌEЪЧBCжаЕуЃЌЁїAODЕФжмГЄБШЁїAOBЕФжмГЄЖр3cmЃЌдђAEЕФГЄЖШЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌЦНааЫФБпаЮABCDЕФжмГЄЪЧ26cmЃЌЖдНЧЯпACгыBDНЛгкЕуOЃЌACЁЭABЃЌEЪЧBCжаЕуЃЌЁїAODЕФжмГЄБШЁїAOBЕФжмГЄЖр3cmЃЌдђAEЕФГЄЖШЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 3cm | BЃЎ | 4cm | CЃЎ | 5cm | DЃЎ | 8cm |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 гУГпЙцзїЭМДгЁїABCЃЈCBЃМCAЃЉжаВУГівЛИівдABЮЊЕзБпЕФЕШбќЁїABDЃЌВЂЪЙЕУЁїABDЕФУцЛ§ОЁПЩФмДѓЃЈБЃСєзїЭМКлМЃЃЌВЛвЊЧѓаДзїЗЈЁЂжЄУїЃЉ
гУГпЙцзїЭМДгЁїABCЃЈCBЃМCAЃЉжаВУГівЛИівдABЮЊЕзБпЕФЕШбќЁїABDЃЌВЂЪЙЕУЁїABDЕФУцЛ§ОЁПЩФмДѓЃЈБЃСєзїЭМКлМЃЃЌВЛвЊЧѓаДзїЗЈЁЂжЄУїЃЉВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com