

分析 【问题发现】(1)根据等边三角形的性质、全等三角形的判定定理证明△AEC≌△BDC;
(2)根据△AEC≌△BDC,得到∠AEC=∠CDB=120°,计算即可;
【拓展探究】证明△AEC≌△BDC,得到△ECD是等腰直角三角形,根据等腰直角三角形的性质计算;
【解决问题】分点P在AD上方、点P在AB的左侧两种情况,根据相似三角形的性质计算.
解答 解:【问题发现】(1)△AEC≌△BDC,
证明:∵△ACB和△DCE均为等边三角形,
∴∠ECD=∠ACB=60°,
∴∠ECA=∠DCB,
在△AEC和△BDC中,
$\left\{\begin{array}{l}{CE=CD}\\{∠ECA=∠DCB}\\{CA=CB}\end{array}\right.$,
∴△AEC≌△BDC,
故答案为:△BDC;
(2)∠CDB=180°-∠CDE=120°,
∵△AEC≌△BDC,
∴∠AEC=∠CDB=120°,AE=BD,
∴∠AEB=60°,
BE=DE+BD=CE+AE;
故答案为:60°;CE+AE=BE;
【拓展探究】∵CD⊥CE,∠ACB=90°,
∴∠ECA=∠DCB,
∵∠AEB=90°,∠ACB=90°,
∴A、E、C、B四点共圆,
∴∠EAC=∠DBC,
在△AEC和△BDC中,
$\left\{\begin{array}{l}{∠ECA=∠DCB}\\{CA=CB}\\{∠EAC=∠DBC}\end{array}\right.$,
∴△AEC≌△BDC,
∴AE=BD,CE=CD,
∴△ECD是等腰直角三角形,
∴ED=$\sqrt{2}$CE,
∴BE=DE+BD=$\sqrt{2}$CE+AE;
【解决问题】当点P在AD上方时,连接AC、PD,作PH⊥CD交AD的延长线于H,
∵AD=5$\sqrt{2}$,
∴AC=10,
则PC=$\sqrt{A{C}^{2}-A{P}^{2}}$=8,
由拓展探究可知,PD=$\frac{PC-PA}{\sqrt{2}}$=$\sqrt{2}$,
∵PH∥AD,
∴∠DPH=∠ADP,
∴∠DPH=∠ACP,
∴PH=PD×$\frac{4}{5}$=$\frac{4\sqrt{2}}{5}$;
当点P在AB的左侧时,同理PH=$\frac{28\sqrt{2}}{5}$.
点评 本题考查的是等边三角形的性质、等腰直角三角形的性质、勾股定理的应用正方形的性质,掌握相关的判定定理和性质定理是解题的关键,注意分情况讨论思想的灵活运用.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
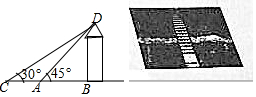 崇圣寺三塔位于大理古城西北部1.5公里处,它是大理历史上规模最为宏大的古刹,南迢丰佑年间曾有殿宇千间,大理国时期是皇家的寺院,崇圣寺三塔由一大二小三阁组成,大塔又名千寻塔.当地群众称它为“文笔塔”,某校数学兴趣小组的同学欲测量主塔垂直于地面的高度BD,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退50.6m至C处,侧得右塔顶端点D的仰角为30°,求该古塔BD的高度($\sqrt{3}≈1.732$,结果保留两位小数).
崇圣寺三塔位于大理古城西北部1.5公里处,它是大理历史上规模最为宏大的古刹,南迢丰佑年间曾有殿宇千间,大理国时期是皇家的寺院,崇圣寺三塔由一大二小三阁组成,大塔又名千寻塔.当地群众称它为“文笔塔”,某校数学兴趣小组的同学欲测量主塔垂直于地面的高度BD,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退50.6m至C处,侧得右塔顶端点D的仰角为30°,求该古塔BD的高度($\sqrt{3}≈1.732$,结果保留两位小数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=2$\sqrt{2}$或4+2$\sqrt{2}$.
如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=2$\sqrt{2}$或4+2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
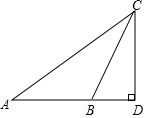 如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)
如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
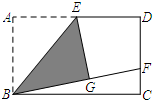 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )| A. | $\frac{13}{3}$ | B. | $\frac{25}{3}$ | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°,底部C的俯角为45°,观察点与楼的水平距离AD为40m,求楼BC的高度(参考数据:sin37°≈0.60;cos37°≈0.80;tan37°≈0.75)
如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°,底部C的俯角为45°,观察点与楼的水平距离AD为40m,求楼BC的高度(参考数据:sin37°≈0.60;cos37°≈0.80;tan37°≈0.75)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com