
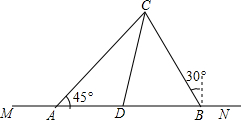
 小明与小红分别住在东西大街相距10(1+$\sqrt{3}$)km的点A与点B处.在小明家北偏东45°与小红家北偏西30°的方向有两条公路交于点C,在点C的南偏西15°的方向上,且在点A与点B之间有一个以点D为圆心的方圆5km的大型批发市场.
小明与小红分别住在东西大街相距10(1+$\sqrt{3}$)km的点A与点B处.在小明家北偏东45°与小红家北偏西30°的方向有两条公路交于点C,在点C的南偏西15°的方向上,且在点A与点B之间有一个以点D为圆心的方圆5km的大型批发市场.分析 (1)作CE⊥AB于E,根据等腰直角三角形得出AE=CE,根据tog∠CBD=tog60°=$\frac{CE}{BE}$=$\sqrt{3}$,求得CE=$\sqrt{3}$BE,从而得出$\sqrt{3}$BE+BE=10(1+$\sqrt{3}$),得出BE=10,进而求得AC=10$\sqrt{6}$,BC=20,然后通过证得△CDB∽△ACB,得出$\frac{CD}{AC}$=$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{20}{10(1+\sqrt{3})}$,从而求得BD的长,进而求得AD的长.
(2)作DN⊥BC于N,通过正弦函数即可求得DN的长,从而判断公路BC不会穿过批发市场.
解答  解:(1)作CE⊥AB于E,
解:(1)作CE⊥AB于E,
∵∠CAD=45°,
∴AE=CE,
∵∠CBD=60°,
∴tog∠CBD=tog60°=$\frac{CE}{BE}$=$\sqrt{3}$,
∴CE=$\sqrt{3}$BE,
∵AB=AE+BE=10(1+$\sqrt{3}$),即$\sqrt{3}$BE+BE=10(1+$\sqrt{3}$),
∴BE=10,
∴AE=CE=10$\sqrt{3}$,
∴AC=$\sqrt{A{E}^{2}+E{C}^{2}}$=10$\sqrt{6}$,BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=20,
∵∠ACE=45°∠ECD=15°,
∴∠ACD=30°,
∴∠CDB=75°,
∵∠CAD=45°,∠CBD=60°,
∴∠ACB=75°,
∴∠CDB=∠ACB,
∵∠CBD=∠ABC,
∴△CDB∽△ACB,
∴$\frac{CD}{AC}$=$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{20}{10(1+\sqrt{3})}$,
∴BD=$\frac{2}{1+\sqrt{3}}$×20=20$\sqrt{3}$-20=20($\sqrt{3}$-1),
∴AD=AB-BD=10(1+$\sqrt{3}$)-20($\sqrt{3}$-1)=30-10$\sqrt{3}$.
答:A和C、A和D之间的距离分别为10$\sqrt{6}$、10(3-$\sqrt{3}$).
(2)作DN⊥BC于N,
∴DN=DB•sin60°=20($\sqrt{3}$-1)×$\frac{\sqrt{3}}{2}$=30-10$\sqrt{3}$>5,
∴公路BC不会穿过批发市场.
点评 题考查解直角三角形的应用,解答此题的关键是构造出直角三角形,利用直角三角形的性质解答.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,MN是圆柱底面的直径,MP是圆柱的高,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,现将圆柱侧面沿MP剪开,所得的侧面展开图可以是( )
如图,MN是圆柱底面的直径,MP是圆柱的高,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,现将圆柱侧面沿MP剪开,所得的侧面展开图可以是( )| A. |  | B. | 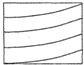 | C. |  | D. | 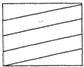 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
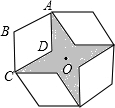 如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=1,则图中阴影部分的面积为3-$\sqrt{3}$.
如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=1,则图中阴影部分的面积为3-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两条直线被第三条直线所截,则同旁内角互补 | |
| B. | 点到直线的距离是指直线外一点到这条直线的垂线段 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | 同一平面内,若直线a∥b,a⊥c,则b⊥c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两个工程队共同开凿一条隧道,甲对按一定的工作效率先施工,一段时间后,乙队从隧道的另一端按一定的工作效率加入施工,中途乙队遇到碎石层,工作效率降低,当乙队完成碎石层时恰好隧道被打通,此时甲队工作了50天.设甲、乙两队各自开凿隧道的长度为y(米),甲对的工作时间为x(天),y与x之间的函数图象如图所示.
甲、乙两个工程队共同开凿一条隧道,甲对按一定的工作效率先施工,一段时间后,乙队从隧道的另一端按一定的工作效率加入施工,中途乙队遇到碎石层,工作效率降低,当乙队完成碎石层时恰好隧道被打通,此时甲队工作了50天.设甲、乙两队各自开凿隧道的长度为y(米),甲对的工作时间为x(天),y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com