
分析 设窗口A到地面的高度AD为xm,根据题意在直角三角形ABD和直角三角形ACD中,利用锐角三角函数用含x的代数式分别表示线段BD和线段CD的长,再根据BD-CD=BC=6列出方程,解方程即可.
解答 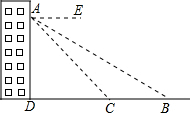 解:设窗口A到地面的高度AD为xm.
解:设窗口A到地面的高度AD为xm.
由题意得:∠ABC=30°,∠ACD=45°,BC=20m.
∵在Rt△ABD中,BD=$\frac{AD}{tan30°}$=$\sqrt{3}$xm,
在Rt△ADC中,CD=$\frac{AD}{tan45°}$=xm,
∵BD-CD=BC=20,
∴$\sqrt{3}$x-x=20,
∴x=10$\sqrt{3}$+10≈27.3.
答:窗口A到地面的高度AD为27.3米.
故答案为:27.3米.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AC$\stackrel{∥}{=}$BD.求证:OA=OB,OC=OD.
已知:如图,AC$\stackrel{∥}{=}$BD.求证:OA=OB,OC=OD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com