
����Ŀ����֪�����κ���![]() ��
��![]() ͼ��Ķ���ֱ�ΪA��B������m��aΪʵ��������C������Ϊ��0��
ͼ��Ķ���ֱ�ΪA��B������m��aΪʵ��������C������Ϊ��0��![]() ����
����
��1�����жϺ���![]() ��ͼ���Ƿ���C����˵�����ɣ�
��ͼ���Ƿ���C����˵�����ɣ�
��2����mΪ����ʵ��ʱ������![]() ��ͼ��ʼ�վ�����C����a��ֵ��
��ͼ��ʼ�վ�����C����a��ֵ��
��3���ڣ�2���������£����ڲ�Ψһ��xֵ����x����ʱ������![]() ��ֵ��С�Һ���
��ֵ��С�Һ���![]() ��ֵ����
��ֵ����
��ֱ��д��m�ķ�Χ��
�ڵ�PΪx��������ԭ��O������һ�㣬����P��y���ƽ���ߣ��뺯��![]() ��
��![]() ��ͼ��ֱ��ཻ�ڵ�D��E����˵��
��ͼ��ֱ��ཻ�ڵ�D��E����˵��![]() ��ֵֻ���P��λ���йأ�
��ֵֻ���P��λ���йأ�

���𰸡���1������y1��ͼ����C������������2��![]() ����3����
����3����![]() ���ڼ�����
���ڼ�����
��������
��1��ȡx=0ʱ�������![]() ��˵������
��˵������![]() ��ͼ����C��
��ͼ����C��
��2������C��0��![]() ������
������![]() ��
��![]() �����a��ֵ��
�����a��ֵ��
��3����ֻҪ![]() �ĶԳ���ʼ����
�ĶԳ���ʼ����![]() �ĶԳ����Ҳ࣬��������Ŀ��Ҫ�ó�m�ķ�Χ��
�ĶԳ����Ҳ࣬��������Ŀ��Ҫ�ó�m�ķ�Χ��
�����P��������![]() ��0�������DE=
��0�������DE=![]() �����ù��ɶ������AB=
�����ù��ɶ������AB=![]() ������˵������.
������˵������.
��1������![]() ��ͼ����C�� �������£�
��ͼ����C�� �������£�
��x=0ʱ��![]() =
=![]() =
=![]() ��
��
�ຯ��![]() ��ͼ����C��
��ͼ����C��
��2������C��0��![]() ������
������![]() �ã�
�ã�
![]() ����
����![]() ����mΪ����ʵ��ʱ������
����mΪ����ʵ��ʱ������![]() ��ͼ��ʼ�վ�����C��
��ͼ��ʼ�վ�����C��
��![]() �ij�����m�أ�
�ij�����m�أ�
��![]() ����
����![]() ��
��
��3����![]() �ĶԳ���Ϊ��
�ĶԳ���Ϊ��![]() ��
��
![]() �ĶԳ���Ϊ��
�ĶԳ���Ϊ��![]() ��
��
��![]() ��
��
����������ͼ�����£���![]() ʱ��x����ʱ������
ʱ��x����ʱ������![]() ��ֵ��С�Һ���
��ֵ��С�Һ���![]() ��ֵ����
��ֵ����
��![]() ��
��
�����P��������![]() ��0������
��0������![]() =
=![]() ��
��![]() =
=![]() ��
��
��DE=![]() =
=![]() =
=![]()
�ɢٿ�֪��![]() ����DE=
����DE=![]() ��
��
��A����x���ƽ���ߣ���B����y���ƽ���ߣ���ƽ�����ཻ��F��
���F ��������![]() ��
��![]() ����
����
��AF=![]() =
=![]() ��BF=
��BF=![]() =
=![]() ��
��
��AB=![]() =
=![]() ����
����![]() =
=![]() =
=![]() ��
��
��![]() ��ֵֻ���P��λ���йأ�
��ֵֻ���P��λ���йأ�
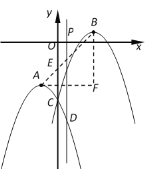


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
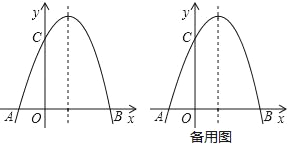
����Ŀ����֪��������y����x2+bx+c������A����1��0����C��0��3������1���������ߵĽ���ʽ����2���������ߵĶԳ����ϣ��Ƿ���ڵ�P��ʹPA+PC��ֵ��С��������ڣ��������P�����꣬��������ڣ���˵�����ɣ���3�����M�������ߵĶԳ����ϣ�����MAC��ֱ��������ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ȫУѧ�������Ķ���������������˲���ѧ����ijһ�������Ķ����µ�ƪ�������Ƴ�����ͳ��ͼ��.


�����ͳ��ͼ���е���Ϣ������������⣺
��1������ѧ��������m��ֵ��
��2���γ���ѧ�������Ķ�ƪ������λ����������
��3������У����1200��ѧ�������ݳ���������Ƹ�Уѧ������һ���������Ķ���ƪ��Ϊ4ƪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л����������е�··��ͣ����λ���ù淶���涨��
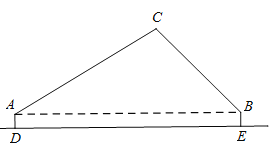
һ���ڳ��е�·��Χ�ڣ��ڲ�Ӱ�����ˡ�����ͨ�е�����£������йز��ſ��Թ滮ͣ����λ.ͣ����λ�����з�ʽ�����֣���ͼ��ʾ��
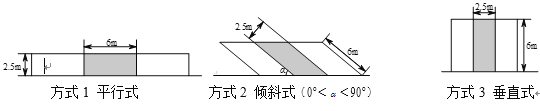
����˫��ͨ�е�·��·����![]() �����ϵģ�����������ͣ����λ��·����
�����ϵģ�����������ͣ����λ��·����![]() ��
��![]() �ģ����ڵ�����ͣ����λ��·����
�ģ����ڵ�����ͣ����λ��·����![]() �����µģ�������ͣ����λ��
�����µģ�������ͣ����λ��
�����涨С��ͣ����λ����λ��![]() �ף���λ��
�ף���λ��![]() �ף�
�ף�
�ġ����ó��е�··�ڻ�����ͣ����λ����������ͨ�еĵ�·����Ӧ��С��![]() ��.
��.
���������Ĺ涨���ڲ����dz�λ����ߺͳ�������ߵĿ��ȵ�����£������һ��·����Ϊ![]() ��˫��ͨ�г�������ͬһ�����з�ʽ��С��ͣ����λ����ش��������⣺
��˫��ͨ�г�������ͬһ�����з�ʽ��С��ͣ����λ����ش��������⣺
��1�����ڸõ�·��������ͣ����λ�����з�ʽΪ ��
��2�������ε�·��![]() �ף���ô�ڵ�·���������������ͣ����λ ��.
�ף���ô�ڵ�·���������������ͣ����λ ��.
(�ο����ݣ�![]() ��
��![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
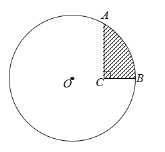
����Ŀ����ͼ����O�İ뾶Ϊ![]() ��A��BΪ��O�����㣬CΪ��O��һ�㣬AC��BC��AC=
��A��BΪ��O�����㣬CΪ��O��һ�㣬AC��BC��AC=![]() ��BC=
��BC=![]() ��
��
��1���жϵ�O��C��B��λ�ù�ϵ��
��2����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��AB����CD��E����F��![]() ���е㣬CF��AB��I������BD��AC��AD��
���е㣬CF��AB��I������BD��AC��AD��
��1����֤��BI��BD��
��2����OI��1��OE��2�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳����ۼס�������Ʒ�ƿյ�����֪ÿ̨����Ʒ�ƿյ��Ľ��۱�ÿ̨����Ʒ�ƿյ��Ľ��۸�20������7200Ԫ����������Ʒ�ƿյ���������3000Ԫ�����ļ���Ʒ�ƿյ�������2̨��
��1����ס�������Ʒ�ƿյ��Ľ����ۣ�
��2�����̳����ò�����16000Ԫ�����ס�������Ʒ�ƿյ���10̨�������ۣ����м���Ʒ�ƿյ����ۼ�Ϊ2500Ԫ��̨������Ʒ�ƿյ����ۼ�Ϊ3500Ԫ��̨����������̳����һ�ֽ���������ʹ����������10̨�յ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �������ȡһ��С��Ȼ��Żأ��������ȡһ����
�������ȡһ��С��Ȼ��Żأ��������ȡһ����
���û���״ͼ���б��ķ������������¼��ĸ��ʣ�
��1������ȡ����С������ͬ��
��2������ȡ����С���ŵĺ͵���4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧС���ڽ����ˮƽ�յ��϶����˻����в��ʵ�飮��ͼ����̨����Ƿֱ����A��Bλ�ã��������߾�Ϊ1�ף���![]() �ף�����̨��������50�ף���AB=50�ף�����ijһʱ�����˻�λ�ڵ�C (��C���A��B��ͬһƽ���ڣ���A�����������Ϊ
�ף�����̨��������50�ף���AB=50�ף�����ijһʱ�����˻�λ�ڵ�C (��C���A��B��ͬһƽ���ڣ���A�����������Ϊ![]() ��B�����������Ϊ
��B�����������Ϊ![]() �����ο����ݣ�
�����ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1�����ʱ�����˻�����ظ߶ȣ�����λ���ף��������������
��2�����˻���ˮƽ�����������2����F����F���A��B��C��ͬһƽ���ڣ�����ʱ��A��������˻�������Ϊ![]() �������˻�ˮƽ���е�ƽ���ٶȣ�����λ����/�룬�������������
�������˻�ˮƽ���е�ƽ���ٶȣ�����λ����/�룬�������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com