
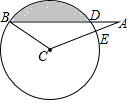
 如图,在∠ABC中,∠ACB=130°,∠BAC=20°,BC=4,以点C为圆心,CB长为半径的圆交AB于点D,交AC于点E.
如图,在∠ABC中,∠ACB=130°,∠BAC=20°,BC=4,以点C为圆心,CB长为半径的圆交AB于点D,交AC于点E.分析 (1)作CH⊥AB于H,在Rt△BCH中利用30度性质即可求出BH,再根据垂径定理可以求出BD;
(2)连接CD,求出∠BCD=120°,阴影部分的面积=扇形CBD的面积-△CBD的面积,代入公式计算即可.
解答  解:(1)如图1,作CH⊥AB于H.
解:(1)如图1,作CH⊥AB于H.
∵∠B=180°-∠A-∠ACB=180°-20°-130°=30°,
在Rt△BCH中,∵∠CHB=90°,∠B=30°,BC=4,
∴CH=$\frac{1}{2}$BC=2,BH=$\sqrt{3}$CE=2$\sqrt{3}$,
∵CH⊥BD,
∴DH=BH,
∴BD=2BH=4$\sqrt{3}$.
(2)连接CD,如图2所示:
∵BC=DC,
∴∠CDB=∠B=30°,
∴∠BCD=120°,
∴阴影部分的面积=扇形CBD的面积-△CBD的面积=$\frac{120π×{4}^{2}}{360}$-$\frac{1}{2}$×4$\sqrt{3}$×2=$\frac{16}{3}π$-4$\sqrt{3}$
点评 本题考查垂径定理、直角三角形的性质、扇形面积公式以及三角形面积计算;熟练掌握垂径定理是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
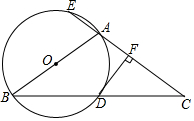 如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
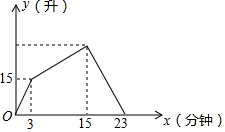 有一个装有进、出水管的容器,先只开进水管,3分钟后,同时打开进、出水管,当容器住满水后,关闭进水管,只打开出水管,直至把容器内水全部放完,在整个过程中容器内水量y(升)与时间x(分钟)之间的函数关系如图所示,那么容器的容积为30升.
有一个装有进、出水管的容器,先只开进水管,3分钟后,同时打开进、出水管,当容器住满水后,关闭进水管,只打开出水管,直至把容器内水全部放完,在整个过程中容器内水量y(升)与时间x(分钟)之间的函数关系如图所示,那么容器的容积为30升.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com