
��•һ��ͯ�ڣ�С�ĵ������棬��������һ���������MN�����ƿ��ȣ�����ͼ���������滥�ഹֱ��ΧǽOP��OQ֮����һ��յ�MPOQN��MP��OP��NQ��OQ�������������MN����һ�㵽����Χǽ�Ĵ��߶���Χǽ��Χ�ɵľ��ε������ȣ����磺A��B��C�����MN�������㣬����ADOG������BEOH������CFOI��������. ������ѧ����������ƽ��ֱ������ϵ����ͼ��.ͼ��������Ӱ���ֵ�����ֱ��ΪS1��S2��S3�������S2=6����λ��ƽ���ף���OG=GH=HI.
��1����S1��S3��ֵ��
��2����T �����MN�ϵ���һ�㣬д��y����x�ĺ�����ϵʽ��
�����MN�ϵ���һ�㣬д��y����x�ĺ�����ϵʽ��
��3������������MPOQN�ڲ������̻���ѡ���ں����ꡢ�����궼��ż���ĵ㴦��ֲ��ľ������߽��ϵĵ���⣩����֪MP=2�ף�NQ=3��.��һ������ֲ���ٿû�ľ��
��1�� ����2��
����2�� ����3��17.
����3��17.
���������������1������ADOG������BEOH������CFOI���������з�������⼴��.
��2���ɵ�MN����һ�㵽����Χǽ�Ĵ��߶���Χǽ��Χ�ɵľ��ε���������ʽ�ɵ�.
��3��������MPOQN�����������ĵ�һһ�г��������.
����������⣺��1���߾���ADOG������BEOH������CFOI�������ȣ���OG=GH=HI��
�� .
.
�֡�S2=6����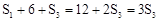 �����
����� .
.
��2���ߵ�T �����MN�ϵ���һ�㣬
�����MN�ϵ���һ�㣬
��������MN����һ�㵽����Χǽ�Ĵ��߶���Χǽ��Χ�ɵľ��ε������ȵ� .
.
��y����x�ĺ�����ϵʽΪ .
.
��3����MP=2��NQ=3��
�൱x=2ʱ��y=18����y=3ʱ��x=12.
�ߺ����ꡢ�����궼��ż�����൱x=4��6��8��10ʱ��y=9��6�� .
.
������MPOQN�����������ĵ�Ϊ��2��2������2��4������2��6������2��8������2��10������2��12������2��14������2��16������4��2������4��4������4��6������4��8������6��2������6��4������8��2������8��4������10��2������17��.
���㣺1.�����������ۺ��⣻2.��ʵ�������к�����ϵʽ��3.�����ϵ�������뷽�̵Ĺ�ϵ��4.������ꣻ5.����˼��ͷ���˼���Ӧ��.


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��C���B��-2��9������ԭ��Գƣ���A���C����y��Գƣ��ҵ�A��˫���� �ϣ����˫���ߵĽ���ʽΪ________________.
�ϣ����˫���ߵĽ���ʽΪ________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����y=x��ͼ���뺯�� ��ͼ���ڵ�һ�����ڽ��ڵ�B����C�Ǻ���
��ͼ���ڵ�һ�����ڽ��ڵ�B����C�Ǻ��� �ڵ�һ����ͼ���ϵ�һ�����㣬����OBC�����Ϊ3ʱ����C�ĺ��������� ����
�ڵ�һ����ͼ���ϵ�һ�����㣬����OBC�����Ϊ3ʱ����C�ĺ��������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ �У���ֱ֪�ߣ죺
�У���ֱ֪�ߣ죺 ��˫����
��˫���� ���ڣ���ȡ��A1������A1��
���ڣ���ȡ��A1������A1�� ��Ĵ��߽�˫�����ڵ�B1������B1��
��Ĵ��߽�˫�����ڵ�B1������B1�� ��Ĵ��߽��ڵ�A2�������������̽��������A2��
��Ĵ��߽��ڵ�A2�������������̽��������A2�� ��Ĵ��߽�˫�����ڵ�B2������B2��
��Ĵ��߽�˫�����ڵ�B2������B2�� ��Ĵ��߽��ڵ�A3�������������εõ��ϵĵ�A1��A2��A3������An�������ǵ�An�ĺ�����Ϊ
��Ĵ��߽��ڵ�A3�������������εõ��ϵĵ�A1��A2��A3������An�������ǵ�An�ĺ�����Ϊ ����
���� ����
���� = ��
= �� = ����Ҫ�������������εؽ�����ȥ����
= ����Ҫ�������������εؽ�����ȥ���� ����ȡ��ֵ��__________
����ȡ��ֵ��__________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ��y=x��1�뷴��������y= ��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m����
��ͼ����A��B���㣬��x�ύ�ڵ�C����֪��A������Ϊ����1��m����
�����������Ľ���ʽ��
������P��n��1���Ƿ���������ͼ����һ�㣬����P��PE��x���ڵ�E���ӳ�EP��ֱ��AB�ڵ�F�����CEF�������
����B��2,1������xΪ��ֵʱ��һ�κ�����ֵ���ڷ�����������ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����A��B�ֱ��� �ᣬ
�ᣬ ���ϣ���D�ڵ�һ�����ڣ�DC��
���ϣ���D�ڵ�һ�����ڣ�DC�� ���ڵ�C��AO=CD=2��AB=DA=
���ڵ�C��AO=CD=2��AB=DA= ������������
������������ ��ͼ���CD���е�E��
��ͼ���CD���е�E��
��1����֤����AOB�ա�DCA��
��2���� ��ֵ��
��ֵ��
��3����BFG�͡�DCA����ij������ĶԳƣ����е�F�� ���ϣ����жϵ�G�Ƿ��ڷ�����������ͼ���ϣ���˵�����ɡ���
���ϣ����жϵ�G�Ƿ��ڷ�����������ͼ���ϣ���˵�����ɡ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪����������y= ��ͼ��������������y=kx��ͼ���ڵ�A��m����2����
��ͼ��������������y=kx��ͼ���ڵ�A��m����2����
��1���������������Ľ���ʽ��������ͼ����һ������B�����ꣻ
��2���Ը���ͼ��д������ʽ ��kx�Ľ⼯��
��kx�Ľ⼯��
��3���ڷ���������ͼ�����Ƿ���ڵ�C��ʹ��OACΪ�ȱ������Σ������ڣ������C�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��Ҫ�����������������һ���������ģ����������1 200 m3�������������ߣ�
(1)����ÿ������x m3������ʱ��Ϊy�죬д��y��x֮��ĺ�����ϵʽ��
(2)��ÿ��������һ������12 m3����5��������������Ҫ������������ꣿ
(3)��(2)������£�����8���ʣ�µ�����Ҫ�ڲ�����6���ʱ����ɣ���ô������Ҫ���Ӷ��������������������ܰ�ʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������������ ��ͼ���ڷ���������
��ͼ���ڷ��������� ��ͼ���ڵ�M��a��1����MN��x���ڵ�N����ͼ��������OMN���������2���������������Ľ���ʽ��
��ͼ���ڵ�M��a��1����MN��x���ڵ�N����ͼ��������OMN���������2���������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com