
不解方程,判断下列一元二次方程的根的情况.
(1)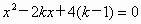 ;
;
(2) ;
;
(3) .
.
|
解: (1)∵a=1,b=-2k,c=4(k-1),∴ 
∴方程有两个实数根. (2) ∵a≠0,∴方程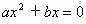 是一元二次方程,此方程是缺少常数项的不完全的一元二次方程,将常数项看作零. 是一元二次方程,此方程是缺少常数项的不完全的一元二次方程,将常数项看作零.
∴ 
∴无论 b取任何实数, 均为非负数, 均为非负数,∴方程有两个实数根. (3)a ≠0,∴方程 是缺少一次项的不完全的一元二次方程,它的一次项系数为b=0. 是缺少一次项的不完全的一元二次方程,它的一次项系数为b=0.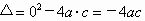 , ,
∴需要讨论 a,c的符号,才能确定Δ的符号.当 c=0时,Δ=0,方程有两个相等的实数根.当 a,c异号时,Δ>0,方程有两个不相等的实数根.当 a,c同号时,Δ<0,方程没有实数根. |
|
运作根的判别式判定根的情况时,要首先把方程变形为一元二次方程的一般形式,然后从求出的判别式的值来判定根的情况,尤其是当方程系数中含有字母时,一般利用配方法将“Δ”化成完全平方式或完全平方式加上 (或减去)一个常数,再根据完全平方式的非负性判断“Δ”的符号,从而判定方程的根的情况,有时还需要对字母进行讨论.这是不解方程判别根的情况的关键. |


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com