
【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】

A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
【答案】D
【解析】∵四边形ABCD是正方形,∴AB=AD,AD∥BC,
∵DE⊥AG,BF∥DE,∴BF⊥AG。∴∠AED=∠DEF=∠BFE=90°。
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,∴∠BAF=∠ADE。
∴△AED≌△BFA(AAS)。故结论A正确。
∴DE=AF,AE=BF,∴DE﹣BF=AF﹣AE=EF。故结论B正确。
∵AD∥BC,∴∠DAE=∠BGF。
∵DE⊥AG,BF⊥AG,∴∠AED=∠GFB=90°。∴△BGF∽△DAE。故结论C正确。
由△ABF∽△AGB得![]() ,即
,即![]() 。
。
由勾股定理得,![]() 。
。
∴![]()
![]() 。
。
∵![]() (只有当∠BAG=300时才相等,由于G是的任意一点,∠BAG=300不一定),
(只有当∠BAG=300时才相等,由于G是的任意一点,∠BAG=300不一定),
∴![]() 不一定等于
不一定等于![]() ,即DE﹣BG=FG不一定成立。故结论D不正确。故选D。
,即DE﹣BG=FG不一定成立。故结论D不正确。故选D。


科目:初中数学 来源: 题型:
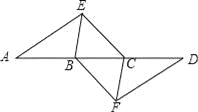
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于多项式3x2﹣2xy2﹣4x+1,下列说法中正确的是( )
A. 是二次四项式 B. 一次项是4x C. 常数项是1 D. 最高次项的系数为2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.

(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com