
| 每人销售台数 | 20 | 17 | 13 | 8 | 5 | 4 |
| 人数 | 1 | 1 | 2 | 5 | 3 | 2 |
分析 (1)根据平均数、中位数和众数的定义求解;
(2)结合实际,应该从调动员工积极性入手分析得出合理的答案.
解答 解:(1)平均数:$\frac{20×1+17×1+13×2+8×5+5×3+4×2}{14}$=9(台),
8台出现了5次,次数最多,所以众数为8台,
14个数据按从小到大的顺序排列后,第7、第8个数都是8,所以中位数是(8+8)÷2=8(台);
(2)每月销售冰箱的定额为8台才比较合适.因为在这儿8既是众数,又是中位数,是大部分人能够完成的台数.若用9台,则只有少量人才能完成,打击了大部分职工的积极性.
点评 此题主要考查了一组数据平均数的求法,以及众数与中位数的求法,又结合了实际问题,此题典型.


科目:初中数学 来源: 题型:选择题
| A. | 8cm2 | B. | 8$\sqrt{3}$cm2 | C. | 16cm2 | D. | 16$\sqrt{3}$cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
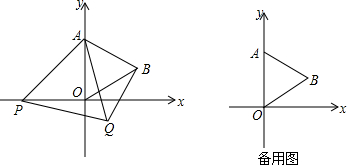
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
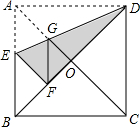 如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB、AC于点E,G,连接GF,下列结论:①AE=AG;②AB=($\sqrt{2}$+1)AE;③GF∥AB;④BE=2OG.则其中正确的结论个数为( )
如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB、AC于点E,G,连接GF,下列结论:①AE=AG;②AB=($\sqrt{2}$+1)AE;③GF∥AB;④BE=2OG.则其中正确的结论个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-7,5) | B. | (7,-5) | C. | (-5,7) | D. | (5,-7) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com