练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知△ABC中，∠ACB＝90°，AC＝BC，点E、F在AB上，∠ECF＝45°．求证：△ACF∽△BEC；

    证明见解析.

    解析试题分析：所求的两个三角形中，∠A、∠B同为45°，∠BCE、∠2均为45°+∠ECF，由此可得两组对应角相等，即可证得所求的三角形相似．
    试题解析：如图：

    ∵AC=BC，∴∠A=∠B
    ∵∠ACB=90°，∴∠A=∠B=45°，
    ∵∠ECF=45°，∴∠ECF=∠B=45°，
    ∴∠ECF+∠1=∠B+∠1
    ∵∠BCE=∠ECF+∠1，∠2=∠B+∠1；
    ∴∠BCE=∠2
    ∵∠A=∠B，∠BCE=∠2，
    ∴△ACF∽△BEC．
    考点: 相似三角形的判定与性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-2，4），（2，1）．
    （1）请在如图所示的网格平面内作出平面直角坐标系；
    （2）请作出△ABC关于y轴对称的△A′B′C′；
    （3）若△ADE是△ABC关于点A的位似图形，且E的坐标为（6，-2），则点D的坐标为　   　, 四边形BCED面积是        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整，原题：如图1，在平行四边形ABCD中，点E是BC的中点，点F是线段AE上一点，BF的延长线交射线CD于点G.若＝3，求的值．

    (1)尝试探究：
    在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是________，
    CG和EH的数量关系是________，
    的值是________．
    (2)类比延伸：
    如图2，在原题条件下，若＝m(m＞0)则的值是________(用含有m的代数式表示)，试写出解答过程．
    (3)拓展迁移：
    如图3，梯形ABCD中，DC∥AB，点E是BC的延长线上的一点，AE和BD相交于点F，若＝a，＝b(a＞0，b＞0)则的值是________(用含a、b的代数式表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，矩形ABCD中，以对角线BD为一边构造一个矩形BDEF，使得另一边EF过原矩形的顶点C．

    （1）设Rt△CBD的面积为S1，Rt△BFC的面积为S2，Rt△DCE的面积为S3，则S1      S2+S3（用“＞”、“=”、“＜”填空）；
    （2）写出如图中的三对相似三角形，并选择其中一对进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部，颖颖的头顶及亮亮的眼睛恰在一条直线上时，两人分别标定自己的位置，．然后测出两人之间的距离，颖颖与楼之间的距离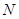（，，在一条直线上），颖颖的身高，亮亮蹲地观测时眼睛到地面的距离．你能根据以上测量数据帮助他们求出住宅楼的高度吗？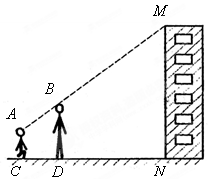

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在Rt△ABC中，AB=AC=4．一动点P从点B出发，沿BC方向以每秒1个单位长度的速度匀速运动，到达点C即停止．在整个运动过程中，过点P作PD⊥BC与Rt△ABC的直角边相交于点D，延长PD至点Q，使得PD=QD，以PQ为斜边在PQ左侧作等腰直角三角形PQE．设运动时间为t秒（t＞0）．

    （1）在整个运动过程中，设△ABC与△PQE重叠部分的面积为S，请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围；
    （2）当点D在线段AB上时，连接AQ、AP，是否存在这样的t，使得△APQ成为等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由；
    （3）当t=4秒时，以PQ为斜边在PQ右侧作等腰直角三角形PQF，将四边形PEQF绕点P旋转，PE与线段AB相交于点M，PF与线段AC相交于点N．试判断在这一旋转过程中，四边形PMAN的面积是否发生变化？若发生变化，求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围；若不发生变化，求出此定值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,且,,求AB的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知△ABD和△CBD关于直线BD对称(点A的对称点是点C)，点E、F分别是线段BC和线段BD上的点，且点F在线段EC的垂直平分线上，联结AF、AE，交BD于点G．
    （1）如图（1），求证：∠EAF=∠ABD；

    图（1）
    （2）如图（2），当AB=AD时，M是线段AG上一点，联结BM、ED、MF，MF的延长线交ED于点N，∠MBF=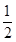∠BAF，AF=AD，试探究线段FM和FN之间的数量关系，并证明你的结论．

    图（2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h为　   　．

    查看答案和解析>>

    同步练习册答案