
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

【答案】①③⑤
【解析】
①利用同角的余角相等,易得∠EAB=∠PAD,再结合已知条件利用SAS可证两三角形全等;
②过B作BF⊥AE,交AE的延长线于F,利用③中的∠BEP=90°,利用勾股定理可求BE,结合△AEP是等腰直角三角形,可证△BEF是等腰直角三角形,再利用勾股定理可求EF、BF;
③利用①中的全等,可得∠APD=∠AEB,结合三角形的外角的性质,易得∠BEP=90°,即可证;
④连接BD,求出△ABD的面积,然后减去△BDP的面积即可;
⑤在Rt△ABF中,利用勾股定理可求AB2,即是正方形的面积.
①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,
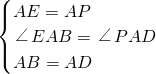 ,
,
∴△APD≌△AEB(SAS);
故此选项成立;
③∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED;
故此选项成立;
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE=![]() =
=![]() =
=![]() ,
,
∴BF=EF=![]() ,
,
故此选项不正确;
④如图,连接BD,在Rt△AEP中,
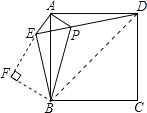
∵AE=AP=1,
∴EP=![]() ,
,
又∵PB=![]() ,
,
∴BE=![]() ,
,
∵△APD≌△AEB,
∴PD=BE=![]() ,
,
∴S△ABP+S△ADP=S△ABD-S△BDP=![]() S正方形ABCD-
S正方形ABCD-![]() ×DP×BE=
×DP×BE=![]() ×(4+
×(4+![]() )-
)-![]() ×
×![]() ×
×![]() =
=![]() +
+![]() .
.
故此选项不正确.
⑤∵EF=BF=![]() ,AE=1,
,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+![]() ,
,
∴S正方形ABCD=AB2=4+![]() ,
,
故此选项正确.
故答案为:①③⑤.


科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: 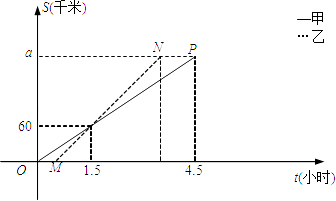
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回. ①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:a2+b2=5c2
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故 ![]() ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人都去同一家超市购买大米各两次,甲每次购买50千克的大米,乙每次购买50元的大米,这两人第一次购买大米时售价为每千克m元,第二次购买大米时售价为每千克n元(m≠n),若规定谁两次购买大米的平均单价低,谁的购买方式就合算,则下列观点正确的是( )
A. 甲的购买方式合算 B. 乙的购买方式合算
C. 甲、乙的购买方式同样合算 D. 不能判断谁的购买方式合算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.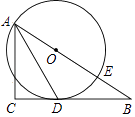
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B的坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.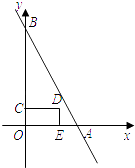
根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,求t的值;
(2)当t=4时,求S的值;
(3)直接写出S与t的函数关系式(不必写出解题过程);
(4)若S=12,则t= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com