
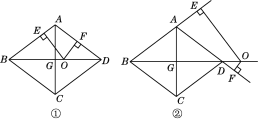
����Ŀ����ͼ���ڱ߳�Ϊ10������ABCD�У��Խ���BD��16���Խ���AC��BD�ཻ�ڵ�G����O��ֱ��BD�ϵĶ��㣬OE��AB��E��OF��AD��F.
(1)��Խ���AC�ij�������ABCD�������
(2)��ͼ�٣�����O�ڶԽ���BD���˶�ʱ��OE��OF��ֵ�Ƿ����仯����˵�����ɣ�
(3)��ͼ�ڣ�����O�ڶԽ���BD���ӳ�����ʱ��OE��OF��ֵ�Ƿ����仯�������䣬��˵�����ɣ����仯����̽��OE��OF֮���������ϵ��
���𰸡���1��12��96 ��2���𰸼����� ��3���𰸼�����
��������
��1���������εĶԽ����ഹֱƽ�����BG�������ù��ɶ�����ʽ���AG��Ȼ�����AC=2AG���㼴�ɵý⣻�ٸ������ε�������ڶԽ��߳˻���һ����ʽ���㼴�ɵý⣻
��2������AO������S��ABD=S��ABO+S��ADO��ʽ���㼴�ɵý⣻
��3������AO������S��ABD=S��ABO-S��ADO��ʽ�������ɵý�.
�⣺(1)������ABCD�У�AG��CG��AC��BD��BG��![]() BD��
BD��![]() ��16��8��
��16��8��
�ɹ��ɶ�����AG��![]() ��
��
����AC��2AG��2��6��12.
��������ABCD�������![]() AC��BD��
AC��BD��![]() ��12��16��96.
��12��16��96.
(2)�������仯���������£���ͼ�٣�����AO����S��ABD��S��ABO��S��AOD��
����![]() BD��AG��
BD��AG��![]() AB��OE��
AB��OE��![]() AD��OF��
AD��OF��
��![]() ��16��6��
��16��6��![]() ��10��OE��
��10��OE��![]() ��10��OF.
��10��OF.
���OE��OF��9.6���Ƕ�ֵ�����䣮
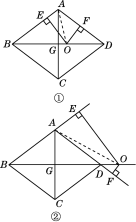
(3)�����仯����ͼ�ڣ�����AO����S��ABD��S��ABO��S��AOD��
����![]() BD��AG��
BD��AG��![]() AB��OE��
AB��OE��![]() AD��OF.
AD��OF.
��![]() ��16��6��
��16��6��![]() ��10��OE��
��10��OE��![]() ��10��OF.
��10��OF.
���OE��OF��9.6���Ƕ�ֵ�����䣮
����OE��OF��ֵ�����仯��OE��OF֮���������ϵΪOE��OF��9.6.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijɭ�ֹ������ŵ�������һ����·���ο��˶�����ͽ�������ų�������������ţ�����һ��ʱ�俪ʼ��Ϣ����Ϣ��0.6Сʱ����ԭ�ټ������ߣ������ͬʱ�����������г��Ӳ�������ǰ�����ţ��������ź���Ϣ0.2Сʱ��Ȼ��ԭ·ԭ�����ٷ��ز��ţ�ͼ�����߷ֱ��ʾ�ס��ҵ����ŵ�·��y��km����׳���ʱ��x��h��֮��ĺ�����ϵͼ����ͼ����Ϣ����������⣮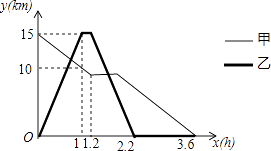
��1���������Ϣǰ�����ŵ�·��y��km�������ʱ��x��h��֮��ĺ�����ϵʽ��
��2����ס��ҵ�һ��������ʱ�䣮
��3��ֱ��д���һص�����ʱ�������ŵ�·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=3ax2+2bx+c��
������a=b=1��c=��1�������������x�ṫ��������ꣻ
������a=b=1���ҵ���1��x��1ʱ����������x������ֻ��һ�������㣬��c��ȡֵ��Χ��
������a+b+c=0����x1=0ʱ����Ӧ��y1��0��x2=1ʱ����Ӧ��y2��0�����жϵ�0��x��1ʱ����������x���Ƿ��й����㣿���У���֤����Ľ��ۣ���û�У��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��C�ֱ���x���ϡ�y���ϣ�CB//OA��OA=8������B������Ϊ(a,b)����b=![]() .
.
��1��ֱ��д����A��B��C�����ꣻ
��2��������P��ԭ��O������x����ÿ��2����λ���ȵ��ٶ������˶�����ֱ��PC���ı���OABC�ֳ������ȵ�������ֹͣ�˶�����P���˶�ʱ����
��3������2���������£���y�����Ƿ����һ��Q������PQ��ʹ������CPQ��������ı���OABC�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��BAC�Ľ�ƽ����AD��BC����D����AB��ijһ��OΪԲ������O��ʹ��O������A�͵�D��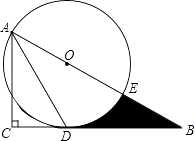
��1���ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɣ�
��2����AC=3����B=30�㣮
�����O�İ뾶��
�����O��AB�ߵ���һ������ΪE�����߶�BD��BE���ӻ�DE��Χ�ɵ���Ӱ���ֵ�ͼ�������������������źͦУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ�������������ɫ��չ����̼���������٣�ij������������һ���������������г������֪������6����ʽ������8��Ůʽ����������ͬ������5����ʽ������4��Ůʽ��������16 000Ԫ��
(1)����ʽ������Ůʽ�����ĵ��ۣ�
(2)������Ҫ����ʽ������Ůʽ������5�������ֵ���������Ҫ22�����������ֵ����ķ��ò�����50 000Ԫ���������м��ֹ��÷������������ò���ʹ�����ܷ�����ͣ���ͷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬�߶�AB�������˵�A��0��2����B��1��0���ֱ���y���x����������ϣ���CΪ�߶�AB���е㣬�ֽ��߶�BA�Ƶ�B��˳ʱ�뷽����ת90��õ��߶�BD��������y=ax2+bx+c��a��0��������D��
��1����ͼ1�����������߾���ԭ��O����a=�� ![]() ��
��
�����D�����꼰�������ߵĽ���ʽ��
������CD���ʣ������������Ƿ���ڵ�P��ʹ�á�POB���BCD���ࣿ�����ڣ�������������������ĵ�P�����꣬�������ڣ���˵�����ɣ�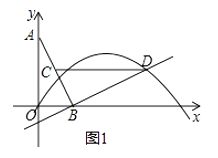
��2����ͼ2������������y=ax2+bx+c��a��0��������E��1��1������Q���������ϣ��������QOB���BCD���࣮������������Q��ĸ�����4������ֱ��д��a��ȡֵ��Χ��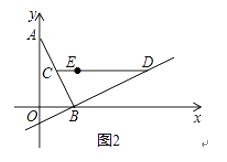
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
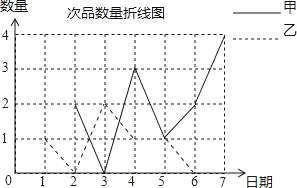
����Ŀ���ס�����������ͬʱ�ӹ�ͬһ��������ָ�������7���Ʒ��ÿ����ֵĴ�Ʒ��������Ƴ����²�������ͳ��ͼ�ͱ�������ͼ������Ϣ������������⣺
���ͳ��������
���� �� | ���� | ��λ�� | ƽ���� | ���� |
�� | �� �� | �� �� | 2 |
|
�� | 1 | 1 | 1 |
|
��Ʒ����ͳ�Ʊ���
���� �� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�� | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
�� | 1 | 0 | 2 | 1 | 1 | 0 | �� �� |
��1����ȫͼ������
��2���ж�˭���ִ�Ʒ�IJ���С��
��3�������Ҽӹ��������30����ִ�Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ˷���ʽ��ѧϰ�У����Dz����˹��켸��ͼ�εķ����о����⣬����ֱ�ۡ�����ļ���ģ�ͣ�����Գ˷���ʽ����ʶ�����⣬���и������ν�ϵ�˼�뷽����������������ڵ�ͳһ�ԣ����ݿ���ѧϰ�ľ��飬����������⣺
��1����ͼ�ٱ߳�Ϊ��x+3����������ֽƬ����ȥһ���߳�Ϊx��������֮��ʣ�ಿ�ֿ�ƴ����һ�������Σ����ص���϶��������������ε����Ϊ�� �����ú�x��ʽ�ӱ�ʾ����
��2���������5�ű߳�Ϊa��������ֽ��4�ų������ֱ�Ϊa��b��a��b���ij�����ֽƬ��3�ű߳�Ϊb������ֽƬ���ִ�����ȡ��������ֽƬ��ÿ��ֽƬ����ȡһ�ţ���ȡ������ЩֽƬƴ��һ�������Σ����ص���϶������ƴ�ɵ������εı߳������Ϊ�� ��
A��a+b��B��a+2b��C��a+3b��D.2a+b��
��3��1���������κ�4����С��ȫ��ͬ��С�����ΰ�ͼ�ڢ����ַ�ʽ�ڷţ���ͼ���У�����������δ��4��С�����θ��Dz��ֵ���������ú�m��n�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com