
 已知:如图.
已知:如图.分析 (1)利用比例的性质进行求解;
(2)利用比例的性质进行求解.
解答 解:(1)∵$\frac{AE}{AC}$=$\frac{AD}{AB}$,
∴$\frac{AE}{AC+AE}$=$\frac{AD}{AB+AD}$,
即$\frac{AE}{CE}$=$\frac{AD}{BD}$;
(2)∵$\frac{AB}{BD}$=$\frac{AC}{CE}$,
∴$\frac{AB}{BD-AB}$=$\frac{AC}{CE-AC}$,
即$\frac{AB}{AD}$=$\frac{AC}{AE}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例. 也考查了比例的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
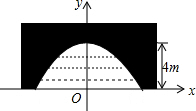 如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.
如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
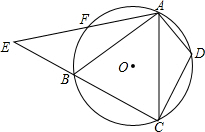 如图,△ABC内接于⊙O,D,F分别是$\widehat{AC}$与$\widehat{AB}$上的点,$\widehat{BF}$=$\widehat{DA}$,连接AF并延长交CB的延长线于点E,连接AD,CD,求证:△CDA∽△ABE.
如图,△ABC内接于⊙O,D,F分别是$\widehat{AC}$与$\widehat{AB}$上的点,$\widehat{BF}$=$\widehat{DA}$,连接AF并延长交CB的延长线于点E,连接AD,CD,求证:△CDA∽△ABE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com