
如图,在⊙O上位于直径AB的异侧有定点C和动点P,AC=AB,点P在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD交PB于D点.

(1)如图1,求证:△PCD∽△ABC;
(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;
(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.
(1)证明见解析(2)当PC是⊙O的直径时,△PCD≌△ABC, ,理由见解析(3)30°
,理由见解析(3)30°
【解析】解:(1)证明:∵AB是⊙O的直径,∴∠ACB=90°。
∵PD⊥CD,∴∠D=90°。∴∠D=∠ACB。
∵∠A与∠P是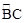 所对的圆周角,∴∠A=∠P,∴△PCD∽△ABC。
所对的圆周角,∴∠A=∠P,∴△PCD∽△ABC。
(2)当PC是⊙O的直径时,△PCD≌△ABC。理由如下:
∵AB,PC是⊙O的半径,∴AB=PC。
∵△PCD∽△ABC,∴△PCD≌△ABC。
画图如下:

(3)∵∠ACB=90°,AC=AB,∴∠ABC=30°。
∵△PCD∽△ABC,∴∠PCD=∠ABC=30°。
∵CP⊥AB,AB是⊙O的直径,∴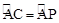 。∴∠ACP=∠ABC=30°。
。∴∠ACP=∠ABC=30°。
∴∠BCD=∠AC﹣∠ACP﹣∠PCD=90°﹣30°﹣30°=30°。
(1)由AB是⊙O的直径,根据直径对的圆周角是直角,即可得∠ACB=90°,又由PD⊥CD,可得∠D=∠ACB,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠P,根据有两角对应相等的三角形相似,即可判定:△PCD∽△ABC。
(2)由△PCD∽△ABC,可知当PC=AB时,△PCD≌△ABC,利用相似比等于1的相似三角形全等即可求得。
(3)由∠ACB=90°,AC=AB,可求得∠ABC的度数,然后利用相似,即可得∠PCD的度数,又由垂径定理,求得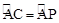 ,然后利用圆周角定理求得∠ACP的度数,从而求得答案。
,然后利用圆周角定理求得∠ACP的度数,从而求得答案。


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
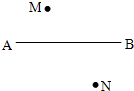 26、如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
26、如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.查看答案和解析>>
科目:初中数学 来源: 题型:
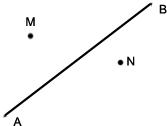 6、如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
6、如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.查看答案和解析>>
科目:初中数学 来源: 题型:

| x2+1 |
| (9-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
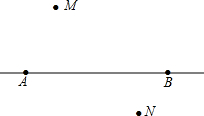 如图,一辆汽车在直线形公路AB上由A向B行驶,M,N是分别位于公路AB两侧的两所学校.
如图,一辆汽车在直线形公路AB上由A向B行驶,M,N是分别位于公路AB两侧的两所学校.查看答案和解析>>
科目:初中数学 来源: 题型:
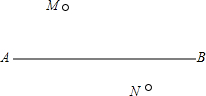 如图,一辆汽车在直线形公路AB上由A向B行驶,M,N分别是位于公路两侧的村庄.行驶到点Q位置时,距离村庄M,N的路程之和最短,请你在图中的公路AB上画出点Q的位置(保留作图痕迹,并用你所学的数学知识说明理由).
如图,一辆汽车在直线形公路AB上由A向B行驶,M,N分别是位于公路两侧的村庄.行驶到点Q位置时,距离村庄M,N的路程之和最短,请你在图中的公路AB上画出点Q的位置(保留作图痕迹,并用你所学的数学知识说明理由).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com