
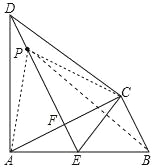
【题目】如图,△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E,连接CE.
(1)求证:AE=CE=BE;
(2)若AB=15cm,BC=9cm,点P是射线DE上的一点.则当点P为何处时,△PBC的周长最小,并求出此时△PBC的周长.

【答案】(1)、证明过程见解析;(2)、当P与E重合时,△PBC的周长最小值为24cm
【解析】
试题分析:(1)、首先证明EA=EC,再证明EC=EB即可解决问题.(2)、先说明P与E重合时△PBC的周长最小,最小值=AB+AC.
试题解析:(1)、∵DA=DC,DF⊥AC,∴AF=CF, ∴DE垂直平分线段AC,∴EA=EC, ∴∠EAC=∠ECA,
∵∠ACB=90°, ∴∠EAC+∠B=90°,∠ECA+∠ECB=90°, ∴∠ECB=∠B, ∴EC=EB=EA.
(2)、连接PB、PC、PA. 要使得△PBC的周长最小,只要PB+PC最小即可. ∵PB+PC=PA+PB≥AB,
∴当P与E重合时,PA+PB最小, ∴△PBC的周长最小值=AB+BC=15+9=24cm.


科目:初中数学 来源: 题型:
【题目】若A(x1 , y1),B(x2 , y2)是一次函数y=ax﹣3x+5图象上的不同的两个点,记W=(x1﹣x2)(y1﹣y2),则当W<0时,a的取值范围是( )
A.a<0
B.a>0
C.a<3
D.a>3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作。根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
A. 44×108 B. 4.4×109 C. 4.4×108 D. 4.4×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠BAC=130°,BC=26,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.求:
(1)∠EAF的度数.
(2)求△AEF的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com