

分析 (1)过点D作DG⊥AB于G,证明Rt△DFN≌Rt△DGM,得MG=NF,AG=AF,再把AM+AN变形即可得出等于2AF;
(2)过点D作DE⊥AB于E,可证明△MDE≌△NDC,得DM=DN,再证明△BDM为等腰三角形,根据直角三角形的性质,30°所对的直角边等于斜边的一半,从而得出AB=18,AM=12,BM=DM=6,同理得:AN=DN=DM=6,即可求得四边形AMDN的周长.
解答 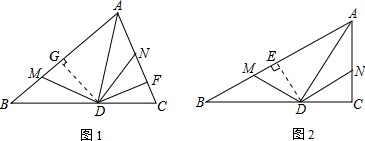 证明:(1)过点D作DG⊥AB于G,如图1,
证明:(1)过点D作DG⊥AB于G,如图1,
∵AD平分∠BAC,DF⊥AC,
∴DF=DG,
在Rt△DFN和Rt△DGM中,
$\left\{\begin{array}{l}DF=DG\\ DN=DM\end{array}\right.$
∴Rt△DFN≌Rt△DGM(HL),
∴MG=NF
又∵AG=AF,
∴AM+AN=AG+MG+AN=AF+NF+AN=2AF;
(2)过点D作DE⊥AB于E,如图2,
在四边形ACDE中,∠EDC=360°-60°-90°-90°=120°,
∴∠EDN+∠MDE=120°,
又∠EDN+∠NDC=120°,
∴∠MDE=∠NDC,
∵AD平分∠BAC,
∴DE=DC,
在△MDE和△NDC中,
$\left\{\begin{array}{l}∠DEM=∠DCN\\ DE=DC\\∠MDE=∠NDC\end{array}\right.$,
∴△MDE≌△NDC(ASA),
∴DM=DN,
∵ND∥AB,
∴∠NDC=∠B=30°,∠DNC=60°,
∴∠MDB=180°-120°-30°=30°,
∴△MDB为等腰三角形,
∴MB=MD,
∴∠ADM=90°,
∴AM=2DM,
在Rt△ABC中,∠B=30°,
∴AB=2AC=18,AM=$\frac{2}{3}$AB=12,BM=$\frac{1}{3}$AB=DM=6,
同理:AN=DN=DM=6,
∴四边形AMDN的周长为12+6+6+6=30.
点评 本题考查了全等三角形的性质和判定,熟练运用角平分线的性质定理、直角三角形的性质,要充分挖掘隐含条件,此类题学生丢分率较高,需注意.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
 [问题提出]
[问题提出]查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D为△ABC的边BC上的一点,DE∥AB,DF∥AC,分别交AC,AB于点E,F,设△CDE,△BDF,四边形DEAF的面积分别为S1,S2,S3,求证:S3=2$\sqrt{{S}_{1}{S}_{2}}$.
如图,D为△ABC的边BC上的一点,DE∥AB,DF∥AC,分别交AC,AB于点E,F,设△CDE,△BDF,四边形DEAF的面积分别为S1,S2,S3,求证:S3=2$\sqrt{{S}_{1}{S}_{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
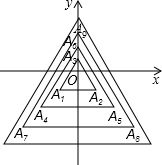 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com