
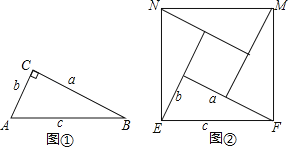
【题目】如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别为△ABC的边AB、AC上的点,BE与CD相交于点O,现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,选择其中2个条件作为题设,余下2个条件作为结论,所有命题中,真命题的个数为( )
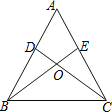
A. .3B. .4C. .5D. 、6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
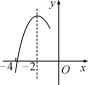
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的点A,B点分别在x轴,y轴上,与双曲线y=![]() 恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )
恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )

A.6B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=x2﹣3与x轴交于AB两点(点A在点B的右侧),与y轴交于点C,连接AC.点Q是线段AC上的动点,过Q作直线l∥x轴,直线1与∠BAC的平分线交于点M,与∠CAx的平分线交于点N.
(1)P是直线AC下方抛物线上一动点,连接PA,PC,当△PAC的面积最大时,求PQ+![]() AM的最小值;
AM的最小值;
(2)如图2,连接MC,NC,当四边形AMCN为矩形时,将△AMN沿着直线AC平移得到△A'M'N',边A'M'所在的直线与y轴交于D点,若△DM'N'为等腰三角形时,求OD的长.
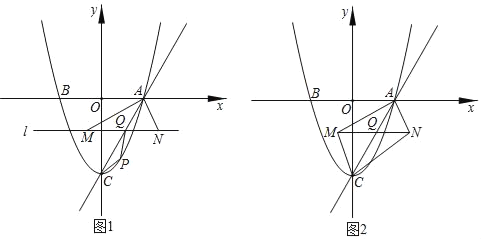
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则![]() 的值是( )
的值是( )
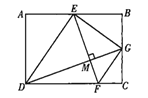
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是种老少皆宜的食品,深受市民欢迎.今年3月份,甲,乙两超市分别用3000元以相同的进价购进质量相同的草莓.甲超市销售方案是:将草莓按大小分类包装销售,其中大草莓400千克,以进价的2倍价格销售,剩下的小草莓以高于进价的10%销售.乙超市销售方案是:不将草莓按大小分类,直接包装销售,价格按甲超市大、小两种草莓售价的平均数定价.若两超市将草莓全部售完,其中甲超市获利2100元(其他成本不计).
(1)草莓进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进行长跑训练,甲和乙所跑的路程S(单位:米)与所用时间t(单位:秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )
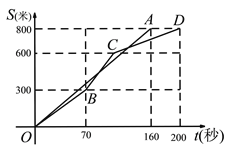
A. 两人从起跑线同时出发,同时到达终点
B. 跑步过程中,两人相遇一次
C. 起跑后160秒时,甲、乙两人相距最远
D. 乙在跑前300米时,速度最慢
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com