
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y= ![]() x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y= ![]() x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示) 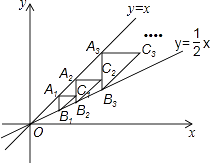
【答案】![]()
【解析】解:∵点A1(2,2),A1B1∥y轴交直线y= ![]() x于点B1 ,
x于点B1 ,
∴B1(2,1)
∴A1B1=2﹣1=1,即△A1B1C1面积= ![]() ×12=
×12= ![]() ;
;
∵A1C1=A1B1=1,
∴A2(3,3),
又∵A2B2∥y轴,交直线y= ![]() x于点B2 ,
x于点B2 ,
∴B2(3, ![]() ),
),
∴A2B2=3﹣ ![]() =
= ![]() ,即△A2B2C2面积=
,即△A2B2C2面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
以此类推,
A3B3= ![]() ,即△A3B3C3面积=
,即△A3B3C3面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
A4B4= ![]() ,即△A4B4C4面积=
,即△A4B4C4面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
…
∴AnBn=( ![]() )n﹣1 , 即△AnBnCn的面积=
)n﹣1 , 即△AnBnCn的面积= ![]() ×[(
×[( ![]() )n﹣1]2=
)n﹣1]2= ![]() .
.
故答案为: ![]()

先根据点A1的坐标以及A1B1∥y轴,求得B1的坐标,进而得到A1B1的长以及△A1B1C1面积,再根据A2的坐标以及A2B2∥y轴,求得B2的坐标,进而得到A2B2的长以及△A2B2C2面积,最后根据根据变换规律,求得AnBn的长,进而得出△AnBnCn的面积即可.本题主要考查了一次函数图象上点的坐标特征以及等腰直角三角形的性质,解决问题的关键是通过计算找出变换规律,根据AnBn的长,求得△AnBnCn的面积.解题时注意:直线上任意一点的坐标都满足函数关系式y=kx+b.


科目:初中数学 来源: 题型:
【题目】如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( ) 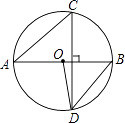
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( ) 
A.4
B.8
C.2 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: 
(1)本次调查的学生共有人,在扇形统计图中,m的值是;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新农村乐园设置了一个秋千场所,如图所,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m) 
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h= 1.5 m
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据: ![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com