

| 1 |
| 2 |
| 1 |
| 2 |
| k1 |
| x |
| 2 |
| x |
|
|
| 2 |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| n |
| 1 |
| n |
| 1 |
| 10 |
|
|
|
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |


 вЛОэИуЖЈЯЕСаД№АИ
вЛОэИуЖЈЯЕСаД№АИ УћаЃзївЕБОЯЕСаД№АИ
УћаЃзївЕБОЯЕСаД№АИ ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
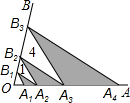 ШчЭМЃЌЕуA1ЃЌA2ЃЌA3ЃЌA4дкЩфЯпOAЩЯЃЌЕуB1ЃЌB2ЃЌB3дкЩфЯпOBЩЯЃЌЧвA1B1ЁЮA2B2ЁЮA3B3ЃЌA2B1ЁЮA3B2ЁЮA4B3ЃЎШєЁїA2B1B2ЃЌЁїA3B2B3ЕФУцЛ§ЗжБ№ЮЊ1ЃЌ4ЃЌдђЭМжаШ§ИівѕгАШ§НЧаЮУцЛ§жЎКЭЮЊ
ШчЭМЃЌЕуA1ЃЌA2ЃЌA3ЃЌA4дкЩфЯпOAЩЯЃЌЕуB1ЃЌB2ЃЌB3дкЩфЯпOBЩЯЃЌЧвA1B1ЁЮA2B2ЁЮA3B3ЃЌA2B1ЁЮA3B2ЁЮA4B3ЃЎШєЁїA2B1B2ЃЌЁїA3B2B3ЕФУцЛ§ЗжБ№ЮЊ1ЃЌ4ЃЌдђЭМжаШ§ИівѕгАШ§НЧаЮУцЛ§жЎКЭЮЊВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
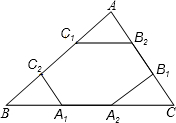 ШчЭМЃЌЕуA1ЁЂA2ЃЌB1ЁЂB2ЃЌC1ЁЂC2ЗжБ№ЪЧЁїABCЕФБпBCЁЂCAЁЂABЕФШ§ЕШЗжЕуЃЌШєЁїABCЕФжмГЄЮЊLЃЌдђСљБпаЮA1A2B1B2C1C2ЕФжмГЄЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌЕуA1ЁЂA2ЃЌB1ЁЂB2ЃЌC1ЁЂC2ЗжБ№ЪЧЁїABCЕФБпBCЁЂCAЁЂABЕФШ§ЕШЗжЕуЃЌШєЁїABCЕФжмГЄЮЊLЃЌдђСљБпаЮA1A2B1B2C1C2ЕФжмГЄЮЊЃЈЁЁЁЁЃЉAЁЂ
| ||
| BЁЂ3L | ||
| CЁЂ2L | ||
DЁЂ
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
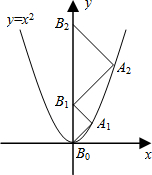 ШчЭМЃЌЕуA1ЁЂA2ЁЂA3ЁЂЁЁЂAnдкХзЮяЯпy=x2ЭМЯѓЕуB1ЁЂB2ЁЂB3ЁЂЁЁЂBnдкyжсЩЯЃЌШєЁїA1B0B1ЁЂЁїA2B1B2ЁЂЁЁЂЁїAnBn-1BnЖМЮЊЕШбќжБНЧШ§НЧаЮЃЈЕуB0ЪЧзјБъдЕуЃЉЃЌдђЁїA2012B2011B2012ЕФбќГЄ=
ШчЭМЃЌЕуA1ЁЂA2ЁЂA3ЁЂЁЁЂAnдкХзЮяЯпy=x2ЭМЯѓЕуB1ЁЂB2ЁЂB3ЁЂЁЁЂBnдкyжсЩЯЃЌШєЁїA1B0B1ЁЂЁїA2B1B2ЁЂЁЁЂЁїAnBn-1BnЖМЮЊЕШбќжБНЧШ§НЧаЮЃЈЕуB0ЪЧзјБъдЕуЃЉЃЌдђЁїA2012B2011B2012ЕФбќГЄ=| 2 |
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌЕуA1ЁЂA2ЁЂA3ЁЂЁЁЂAnдкХзЮяЯпy=x2ЭМЯѓЩЯЃЌЕуB1ЁЂB2ЁЂB3ЁЂЁЁЂBnдкyжсЩЯЃЌШєЁїA1B0B1ЁЂЁїA2B1B2ЁЂЁЁЂЁїAnBn-1BnЖМЮЊЕШбќжБНЧШ§НЧаЮЃЈЕуB0ЪЧзјБъдЕуЃЉЃЌдђЁїA2013B2012B2013ЕФбќГЄ=
ШчЭМЃЌЕуA1ЁЂA2ЁЂA3ЁЂЁЁЂAnдкХзЮяЯпy=x2ЭМЯѓЩЯЃЌЕуB1ЁЂB2ЁЂB3ЁЂЁЁЂBnдкyжсЩЯЃЌШєЁїA1B0B1ЁЂЁїA2B1B2ЁЂЁЁЂЁїAnBn-1BnЖМЮЊЕШбќжБНЧШ§НЧаЮЃЈЕуB0ЪЧзјБъдЕуЃЉЃЌдђЁїA2013B2012B2013ЕФбќГЄ=| 2 |
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
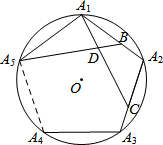 ЃЈ2013•ФЯОЉЖўФЃЃЉШчЭМЃЌЕуA1ЁЂA2ЁЂA3ЁЂA4ЁЂA5дкЁбOЩЯЃЌЧв
ЃЈ2013•ФЯОЉЖўФЃЃЉШчЭМЃЌЕуA1ЁЂA2ЁЂA3ЁЂA4ЁЂA5дкЁбOЩЯЃЌЧв |
| A1A2 |
 |
| A2A3 |
 |
| A3A4 |
 |
| A4A5 |
 |
| A5A1 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com