
 如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2.
如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2.分析 (1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2,HE2=AH2+AE2,再根据菱形的性质,得到等式DH2+DG2=AH2+AE2,最后计算AE的长;
(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,因为∠AEH+∠AHE=90°,∠DHG+∠AHE=90°,可得菱形的一个角为90°,进而判定该菱形为正方形.
解答 (1)解:∵AD=6,AH=2
∴DH=AD-AH=4
∵四边形ABCD是矩形
∴∠A=∠D=90°
∴在Rt△DHG中,HG2=DH2+DG2
在Rt△AEH中,HE2=AH2+AE2
∵四边形EFGH是菱形
∴HG=HE
∴DH2+DG2=AH2+AE2
即42+62=22+AE2
∴AE=$\sqrt{48}$=4$\sqrt{3}$;
(2)证明:∵AH=2,DG=2,
∴AH=DG,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△DHG和Rt△AEH中,
$\left\{\begin{array}{l}{HG=EH}\\{\;}\\{DG=AH}\end{array}\right.$,
∴Rt△DHG≌Rt△AEH(HL),
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∵四边形EFGH是菱形,
∴四边形EFGH是正方形.
点评 本题主要考查了矩形、菱形的性质以及正方形的判定,解决问题的关键是掌握:矩形的四个角都是直角,菱形的四条边都线段,有一个角为直角的菱形是正方形.在解题时注意,求直角三角形的边长时,一般都需要考虑运用勾股定理进行求解.


科目:初中数学 来源: 题型:选择题
| A. | 16(1+a)2=25 | B. | 25(1-2a)=16 | C. | 25(1-a)2=16 | D. | 25(1-a2)=16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
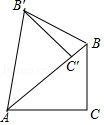 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠C′B′B的度数为( )| A. | 40° | B. | 50° | C. | 70° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.28×10-6米 | B. | 2.8×10-8米 | C. | 2.8×10-7米 | D. | 2.8×10-6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 单价(台/元) |
| 电视机 | 5000 |
| 洗衣机 | 2000 |
| 空调 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
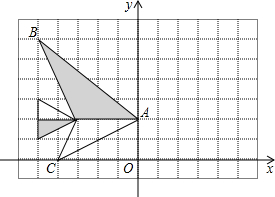 如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.
如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
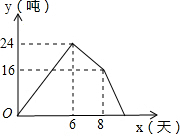 春耕期间,某农资门市部连续8天调进一批农用物资,在开始调进物资的第7天开始销售,若进货期间每天调入物资的数量与销售期间每天销售物资的数量都保持不变,这个门市部的物资存量y(单位:吨)与时间x(单位:天)之间的函数关系如图所示,则该门市部这次农用物资活动(从开始进货到销售完毕)所用时间是10天.
春耕期间,某农资门市部连续8天调进一批农用物资,在开始调进物资的第7天开始销售,若进货期间每天调入物资的数量与销售期间每天销售物资的数量都保持不变,这个门市部的物资存量y(单位:吨)与时间x(单位:天)之间的函数关系如图所示,则该门市部这次农用物资活动(从开始进货到销售完毕)所用时间是10天.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
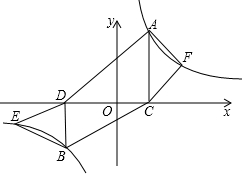 如图,点A和点F,点B和点E分别是反比例函数y=$\frac{4}{x}$图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为12-6$\sqrt{3}$.
如图,点A和点F,点B和点E分别是反比例函数y=$\frac{4}{x}$图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为12-6$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com