
| A. | 正数 | B. | 负数 | C. | 零 | D. | 非负数 |
分析 首先将原式通分再进行变形,进而利用已知公式分析得出答案.
解答 解:$\frac{1}{a}$$+\frac{1}{b}$$+\frac{1}{c}$=$\frac{bc}{abc}$+$\frac{ac}{abc}$+$\frac{ab}{abc}$
=$\frac{bc+ac+ab}{abc}$
∵(x+y+z)2=x2+y2+z2+2(xy+yz+xz),a+b+c=0,
∴(a+b+c)2=a2+b2+c2+2(ab+bc+ac)=0,
∴a2+b2+c2=-2(ab+bc+ac),
∵abc=6,∴a,b,c都不为0,
∴ab+bc+ac<0,
∴$\frac{bc+ac+ab}{abc}$=$\frac{ba+bc+ac}{6}$<0.
故选:B.
点评 此题主要考查了完全平方公式的应用,正确将原式变形是解题关键.


科目:初中数学 来源: 题型:解答题
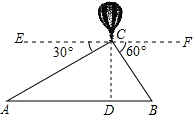 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com