
【题目】点A在数轴上对应的数为﹣3,点B对应的数为2.
(1)如图1点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣5的解,在数轴上是否存在点P使PA+PB=
x﹣5的解,在数轴上是否存在点P使PA+PB=![]() BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
BC+AB?若存在,求出点P对应的数;若不存在,说明理由;
(2)如图2,若P点是B点右侧一点,PA的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,有两个结论:①PM﹣![]() BN的值不变;②
BN的值不变;②![]() BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值
![]()
【答案】(1)存在满足条件的点P,对应的数为﹣![]() 和
和![]() ;(2)正确的结论是:PM﹣
;(2)正确的结论是:PM﹣![]() BN的值不变,且值为2.5.
BN的值不变,且值为2.5.
【解析】
(1)先利用数轴上两点间的距离公式确定出AB的长,然后求得方程的解,得到C表示的点,由此求得![]() BC+AB=8设点P在数轴上对应的数是a,分①当点P在点a的左侧时(a<﹣3)、②当点P在线段AB上时(﹣3≤a≤2)和③当点P在点B的右侧时(a>2)三种情况求点P所表示的数即可;(2)设P点所表示的数为n,就有PA=n+3,PB=n﹣2,根据已知条件表示出PM、BN的长,再分别代入①PM﹣
BC+AB=8设点P在数轴上对应的数是a,分①当点P在点a的左侧时(a<﹣3)、②当点P在线段AB上时(﹣3≤a≤2)和③当点P在点B的右侧时(a>2)三种情况求点P所表示的数即可;(2)设P点所表示的数为n,就有PA=n+3,PB=n﹣2,根据已知条件表示出PM、BN的长,再分别代入①PM﹣![]() BN和②
BN和②![]() PM+
PM+![]() BN求出其值即可解答.
BN求出其值即可解答.
(1)∵点A在数轴上对应的数为﹣3,点B对应的数为2,
∴AB=5.
解方程2x+1=![]() x﹣5得x=﹣4.
x﹣5得x=﹣4.
所以BC=2﹣(﹣4)=6.
所以.
设存在点P满足条件,且点P在数轴上对应的数为a,
①当点P在点a的左侧时,a<﹣3,
PA=﹣3﹣a,PB=2﹣a,所以AP+PB=﹣2a﹣1=8,
解得a=﹣![]() ,﹣
,﹣![]() <﹣3满足条件;
<﹣3满足条件;
②当点P在线段AB上时,﹣3≤a≤2,PA=a﹣(﹣3)=a+3,PB=2﹣a,
所以PA+PB=a+3+2﹣a=5≠8,不满足条件;
③当点P在点B的右侧时,a>2,PA=a﹣(﹣3)=a+3,PB=a﹣2.,
所以PA+PB=a+3+a﹣2=2a+1=8,解得:a=![]() ,
,![]() >2,
>2,
所以,存在满足条件的点P,对应的数为﹣![]() 和
和![]() .
.
(2)设P点所表示的数为n,
∴PA=n+3,PB=n﹣2.
∵PA的中点为M,
∴PM=![]() PA=
PA=![]() .
.
N为PB的三等分点且靠近于P点,
∴BN=![]() PB=
PB=![]() ×(n﹣2).
×(n﹣2).
∴PM﹣![]() BN=
BN=![]() ﹣
﹣![]() ×
×![]() ×(n﹣2),
×(n﹣2),
=![]() (不变).
(不变).
②![]() PM+
PM+![]() BN=
BN=![]() +
+![]() ×
×![]() ×(n﹣2)=
×(n﹣2)=![]() n﹣
n﹣![]() (随P点的变化而变化).
(随P点的变化而变化).
∴正确的结论是:PM﹣![]() BN的值不变,且值为2.5.
BN的值不变,且值为2.5.


科目:初中数学 来源: 题型:
【题目】先阅读下面的村料,再分解因式.
要把多项式![]() 分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
![]() .
.
这时,由于![]() 中又有公困式
中又有公困式![]() ,于是可提公因式
,于是可提公因式![]() ,从而得到
,从而得到![]() ,因此有
,因此有
![]()
![]()
![]()
![]() .
.
这种因式分解的方法叫做分组分解法,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来因式分解.
请用上面材料中提供的方法因式分解:
![]()
![]() 请你完成分解因式下面的过程
请你完成分解因式下面的过程![]()
![]() ______
______
![]() ;
;
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.

(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
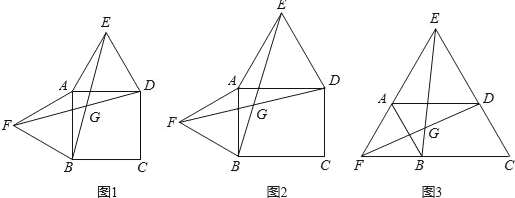
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用数轴解决问题:我们知道,若数轴上点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则
,则![]() 、
、![]() 两点间的距离记作
两点间的距离记作![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() = ;
= ;
(2)若数轴上一点![]() 表示的数是
表示的数是![]() ,
,![]() ,则
,则![]() = ;
= ;
(3)若点![]() 表示的数是
表示的数是![]() ,已知
,已知![]() ,点
,点![]() 在
在![]() 的左边,
的左边,![]() ,点
,点![]() 在点
在点![]() 的右边,
的右边,![]() ,点
,点![]() 以每秒
以每秒![]() 的速度向右移动,同时点
的速度向右移动,同时点![]() 、点
、点![]() 分别以每秒
分别以每秒![]() 、
、![]() 的速度向左移动.设移动时间为
的速度向左移动.设移动时间为![]() 秒,那么
秒,那么![]() 是否有最小值?若有,求出最小值并写出此时
是否有最小值?若有,求出最小值并写出此时![]() 的取值范围;若没有,请说明理由.
的取值范围;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com