
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k<![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).

【答案】(1)AAS;(2)AB=4;(3)![]() .
.
【解析】
试题分析:(1)作AF⊥BC,根据已知条件易得∠AFB=∠BEA,∠DAB=∠ABD,AB=AB,根据AAS可判断出△ABF≌△BAE;(2)连接AD,作CG⊥AF,易得tan∠DAE=![]() ,再由tan∠F=tan∠DAE,求出CG,再证△DCG∽△ACE,根据相似三角形的性质即可求出AC;(3)过点D作DG⊥BC,设DG=a,在Rt△ABH,Rt△ADN,Rt△ABH中分别用a,k表示出AB=2a(k+1),BH=
,再由tan∠F=tan∠DAE,求出CG,再证△DCG∽△ACE,根据相似三角形的性质即可求出AC;(3)过点D作DG⊥BC,设DG=a,在Rt△ABH,Rt△ADN,Rt△ABH中分别用a,k表示出AB=2a(k+1),BH=![]() a(k+1),BC=2BH=2
a(k+1),BC=2BH=2![]() a(k+1),CG=
a(k+1),CG=![]() a(2k+1),DN=
a(2k+1),DN=![]() ka,最后用△NDE∽△GDC,求出AE,EC即可.
ka,最后用△NDE∽△GDC,求出AE,EC即可.
试题解析:证明:(1)如图2,
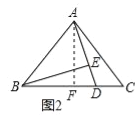
作AF⊥BC,
∵BE⊥AD,∴∠AFB=∠BEA,
在△ABF和△BAE中,
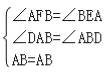 ,
,
∴△ABF≌△BAE(AAS),
∴BF=AE
∵AB=AC,AF⊥BC,
∴BF=![]() BC,
BC,
∴BC=2AE,
故答案为AAS
(2)如图3,
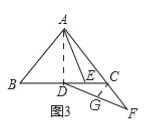
连接AD,作CG⊥AF,
在Rt△ABC中,AB=AC,点D是BC中点,
∴AD=CD,
∵点E是DC中点,
∴DE=![]() CD=
CD=![]() AD,
AD,
∴tan∠DAE=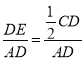 =
=![]() ,
,
∵AB=AC,∠BAC=90°,点D为BC中点,
∴∠ADC=90°,∠ACB=∠DAC=45°,
∴∠F+∠CDF=∠ACB=45°,
∵∠CDF=∠EAC,
∴∠F+∠EAC=45°,
∵∠DAE+∠EAC=45°,
∴∠F=∠DAE,
∴tan∠F=tan∠DAE=![]() ,
,
∴![]() ,
,
∴CG=![]() ×2=1,
×2=1,
∵∠ACG=90°,∠ACB=45°,
∴∠DCG=45°,
∵∠CDF=∠EAC,
∴△DCG∽△ACE,
∴![]() ,
,
∵CD=![]() AC,CE=
AC,CE=![]() CD=
CD=![]() AC,
AC,
∴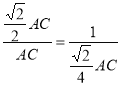 ,
,
∴AC=4;
∴AB=4;
(3)如图4,
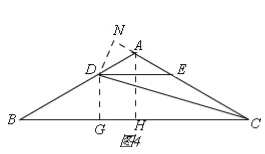
过点D作DG⊥BC,设DG=a,
在Rt△BGD中,∠B=30°,
∴BD=2a,BG=![]() a,
a,
∵AD=kDB,
∴AD=2ka,AB=BD+AD=2a+2ka=2a(k+1),
过点A作AH⊥BC,
在Rt△ABH中,∠B=30°.
∴BH=![]() a(k+1),
a(k+1),
∵AB=AC,AH⊥BC,
∴BC=2BH=2![]() a(k+1),
a(k+1),
∴CG=BC﹣BG=![]() a(2k+1),
a(2k+1),
过D作DN⊥AC交CA延长线与N,
∵∠BAC=120°,
∴∠DAN=60°,
∴∠ADN=30°,
∴AN=ka,DN=![]() ka,
ka,
∵∠DGC=∠AND=90°,∠AED=∠BCD,
∴△NDE∽△GDC.
∴![]() ,
,
∴![]() ,
,
∴NE=3ak(2k+1),
∴EC=AC﹣AE=AB﹣AE=2a(k+1)﹣2ak(3k+1)=2a(1﹣3k2),
∴![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】妈妈做了一份美味可口的菜品,为了了解菜品的咸淡是否适合,于是妈妈取了一点品尝,属于_________________ (填“普查”或“ 抽样调查”)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
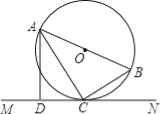
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣3x+![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
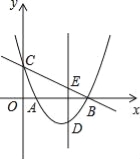
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC
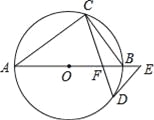
(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形顶角的平分线、底边上的中线、底边上的高__________(也称“_____________”),它们所在的直线都是等腰三角形的_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
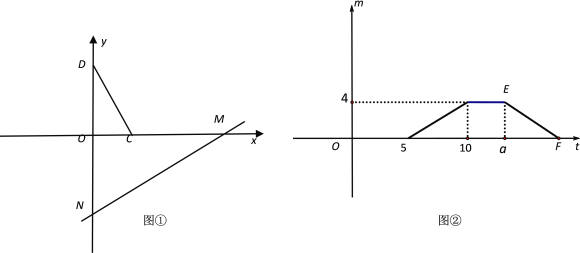
【题目】如图①,将□ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左侧),点D坐标为(0,4),直线MN:y=![]() x-6沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t(s),m与t的函数图像如图②所示.
x-6沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t(s),m与t的函数图像如图②所示.
(1)填空:点C的坐标为 ;在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)
(2)点B的坐标为 ,a= .
(3)求图②中线段EF的函数关系式;
(4)t为何值时,该直线平分□ABCD的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2![]() ,反比例函数y=
,反比例函数y=![]() (x>0)的图象经过OA的中点C,交AB于点D.
(x>0)的图象经过OA的中点C,交AB于点D.

(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com