Question

15．已知，一张矩形纸片ABCD把顶点A和C叠合在一起，得折痕EF（如图）
（1）猜想四边形AECF是什么四边形，并证明你的猜想；
（2）矩形纸片ABCD的边长分别为9cm和3cm，求折痕EF的长．

Answer 1

分析 （1）利用折叠性质得EA=EC，FA=FC，∠1=∠2，再证明∠2=∠3得到EC=FC，则EA=EC=FA=FC，运算可判断四边形AECF是菱形；
（2）连结AC交EF于O点，如图，先利用勾股定理计算出AC=3$\sqrt{10}$，再利用菱形的性质得AC⊥EF，OE=OF，OA=OC=$\frac{3\sqrt{10}}{2}$，然后证明△AOF∽△ABC，则可利用相似比求出OF，从而得到EF的长．

解答 解：（1）四边形AECF是菱形．理由如下：
∵矩形ABCD把顶点A和C叠合在一起，得折痕EF，
∴EA=EC，FA=FC，∠1=∠2，
∵AD∥AB，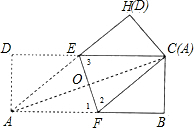
∴∠1=∠3，
∴∠2=∠3，
∴EC=FC，
∴EA=EC=FA=FC，
∴四边形AECF是菱形；
（2）连结AC交EF于O点，如图，
在Rt△ACB中，∵AB=9，BC=3，
∴AC=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$，
∵四边形AECF是菱形，
∴AC⊥EF，OE=OF，OA=OC=$\frac{3\sqrt{10}}{2}$，
∵∠OAF=∠BAC，
∴△AOF∽△ABC，
∴OF：BC=AO：AB，即OF：3=$\frac{3\sqrt{10}}{2}$：9，解得OF=$\frac{\sqrt{10}}{2}$，
∴EF=2OF=$\sqrt{10}$．

点评 本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．熟练掌握矩形的性质和菱形的判定与性质．