
 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, .它的顶点
.它的顶点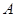 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,
, ,点
,点 从点
从点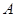 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点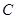 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
 的度数.
的度数. 在
在 上运动时,
上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点 的运动速度.
的运动速度. 与时间
与时间 之间的函数关系式及面积
之间的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标. 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点 沿
沿 边运动时,
边运动时,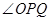 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时,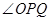 的大小随着时间
的大小随着时间 的增大而减小,当点
的增大而减小,当点 沿这两边运动时,使
沿这两边运动时,使 的点
的点 有几个?请说明理由.
有几个?请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,求点B的坐标。
,求点B的坐标。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
销售单价 (元∕件) (元∕件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |
 、
、 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想 与
与 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式; 
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 与
与 轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则
轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则

 (填“
(填“ ”或“
”或“ ”);
”);查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.-2<a+b+c<0 | B.0<a+b+c<2 | C.-4<a+b+c<0 | D.0<a+b+c<4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com