
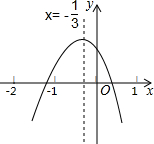 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 根据图象可知顶点在y轴左侧,则a、b的符号相同,从而可以判断①;由函数图象可知x=1时,y<0,x=-1时y>0,对称轴为x=-$\frac{b}{2a}$=-$\frac{1}{3}$,从而可以判断②③是否正确,根据点到对称轴的距离即可判断④.
解答 解:∵二次函数y=ax2+bx+c(a≠0)的顶点在y轴左侧,
∴a、b符号相同,
∴ab>0,故①正确;
∵由图象可知,x=1时,函数值小于0,
∴a+b+c<0,故②正确;
∵-$\frac{b}{2a}$=-$\frac{1}{3}$,
∴a=$\frac{3}{2}$b,
∵由图象可知,x=-1时,函数值大于0,
∴a-b+c>0,
∴$\frac{3}{2}$b-b+c>0,
∴$\frac{b}{2}$+c>0,
∴b+2c>0,故③正确;
∵|-3+$\frac{1}{3}$|=$\frac{8}{3}$.|6+$\frac{1}{3}$|=$\frac{19}{3}$,
∴点(-3,m)离对称轴近,
∴m>n,故④错误;
由上可得①②③正确.
故选A.
点评 本题考查二次函数图象与系数的关系,解题的关键是明确它们之间的关系,利用数形结合的思想解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,小宇用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第10个图案中共有121个黑子.
如图,小宇用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第10个图案中共有121个黑子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
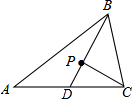 如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.
如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+2$\sqrt{3}$=3$\sqrt{5}$ | B. | 15x3-7x3=8x3 | C. | (-xy)2=-x2y2 | D. | x6÷x2=x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2(x-1)-x-2>1 | B. | 2(x-1)-x+2>1 | C. | 2(x-1)-x-2>4 | D. | 2(x-1)-x+2>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com