练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

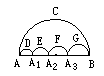
    如图所示中的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点．甲虫沿、、、路线爬行，乙虫沿ACB路线爬行，则下列结论中正确的是

    [　　]

    A．甲先到B点
    B．乙先到B点
    C．甲、乙同时到B点
    D．无法确定
    答案：C
    解析：

    如图:设大半圆半径为R,小圆半径为r1,r2,r3,r4且R=r1+r2+r3+r4因为,,所以甲,乙两小虫同时到达B点,故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在“五个重庆”建设中，为了提高市民的宜居环境，某区规划修建一个文化广场（平面图形如图所示），其中四边形ABCD是矩形，分别以AB、BC、CD、DA边为直径向外作半圆，若整个广场的周长为628米，设矩形的边长AB=y米，BC=x米．（注：取 π=3.14）
    （1）试用含x的代数式表示y；
    （2）现计划在矩形ABCD区域上种植花草和铺设鹅卵石等，平均每平方米造价为428 元，在四个半圆的区域上种植草坪及铺设花岗岩，平均每平方米造价为400元；
    ①设该工程的总造价为W元，求W关于x的函数关系式；
    ②若该工程政府投入1千万元，问能否完成该工程的建设任务？若能，请列出设计方案；若不能，请说明理由；
    ③若该工程在政府投入1千万元的基础上，又增加企业募捐资金64.82万元，但要求矩形的边BC的长不超过AB长的三分之二，且建设广场恰好用完所有资金，问：能否完成该工程的建设任务？若能，请列出所有可能的设计方案；若不能精英家教网，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    在“五个重庆”建设中，为了提高市民的宜居环境，某区规划修建一个文化广场(平面图形如图所示)，其中四边形ABCD是矩形，分别以AB、BC、CD、DA边为直径向外作半圆，若整个广场的周长为628 米，矩形的边长AB=y米，BC=x米， (注：取= 3.14 )  
    (1)试用含x的代数式表示y；    
    (2)现计划在矩形ABCD区域土种植花草和铺设鹅卵石等，平均每平方米造价为428元. 在四个半圆的区域上种植草坪及铺设花岗岩，平均每平方米造价为 400元；
    ①设该工程的总造价为W元，求 W关于x 的函数关系式；
    ②若该工程政府投入1 千万元，问能否完成该工程的建设任务？若能，请列出设计方案，若不能，请说明理由？    
    ③若该工程在政府投入1 千万元的基础上，又增加企业募捐资金64.82万元，但要求矩形的边 BC的长不超过AB长的三分之二，且建设广场恰好用完所有资金，问：能否完成该工程的建设任务？若能，请列出所有可能的设计方案，若不能，请说明理由.    

    查看答案和解析>>

    科目：初中数学 来源：重庆市中考真题 题型：解答题

    在“五个重庆”建设中，为了提高市民的宜居环境，某区规划修建一个文化广场（平面图形如图所示），其中四边形ABCD是矩形，分别以AB、BC、CD、DA边为直径向外作半圆，若整个广场的周长为628m，设矩形的边长AB=y（m），BC=x（m）。（注：取π=3.14）

    （1）试用含x的代数式表示y；
    （2）现计划在矩形ABCD区域上种植花草和铺设鹅卵石等，平均每平方米造价为428元，在四个半圆的区域上种植草坪及铺设花岗岩，平均每平方米造价为400元；
    ①设该工程的总造价为W元，求W关于x的函数关系；
    ②若该工程政府投入1千万元，问能否完成该工程的建设任务？若能，请列出设计方案，若不能，请说明理由？
    ③若该工程政府投入1千万元的基础上，又增加企业募捐资金64.82万元，但要求矩形的边长BC的长不超过AB长的三分之二，且建设广场恰好用完所有资金，问：能否完成该工程的建设任务？若能，请列出所有可能的设计方案，若不能，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源：2012年浙江省杭州市中考数学模拟试卷（48）（解析版） 题型：解答题

    在“五个重庆”建设中，为了提高市民的宜居环境，某区规划修建一个文化广场（平面图形如图所示），其中四边形ABCD是矩形，分别以AB、BC、CD、DA边为直径向外作半圆，若整个广场的周长为628米，设矩形的边长AB=y米，BC=x米．（注：取 π=3.14）
    （1）试用含x的代数式表示y；
    （2）现计划在矩形ABCD区域上种植花草和铺设鹅卵石等，平均每平方米造价为428 元，在四个半圆的区域上种植草坪及铺设花岗岩，平均每平方米造价为400元；
    ①设该工程的总造价为W元，求W关于x的函数关系式；
    ②若该工程政府投入1千万元，问能否完成该工程的建设任务？若能，请列出设计方案；若不能，请说明理由；
    ③若该工程在政府投入1千万元的基础上，又增加企业募捐资金64.82万元，但要求矩形的边BC的长不超过AB长的三分之二，且建设广场恰好用完所有资金，问：能否完成该工程的建设任务？若能，请列出所有可能的设计方案；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案