
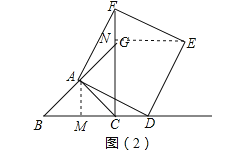
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻBAC=90”ć£¬µćDŌŚÉäĻßBCÉĻ£ØÓėB”¢CĮ½µć²»ÖŲŗĻ£©£¬ŅŌADĪŖ±ß×÷Õż·½ŠĪADEF£¬Ź¹µćEÓėµćBŌŚÖ±ĻßADµÄŅģ²ą£¬ÉäĻßBAÓėÖ±ĻßCFĻą½»ÓŚµćG£®
£Ø1£©ČōµćDŌŚĻ߶ĪBCÉĻ£¬ČēĶ¼£Ø1£©£¬ÅŠ¶Ļ£ŗĻ߶ĪBCÓėĻ߶ĪCGµÄŹżĮæ¹ŲĻµ£ŗ”” ””£¬Ī»ÖĆ¹ŲĻµ£ŗ”” ””£®
£Ø2£©ČēĶ¼£Ø2£©£¬¢ŁČōµćDŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻ£¬£Ø1£©ÖŠÅŠ¶ĻĻ߶ĪBCÓėĻ߶ĪCGµÄŹżĮæ¹ŲĻµÓėĪ»ÖĆ¹ŲĻµŹĒ·ńČŌČ»³ÉĮ¢£¬²¢ĖµĆ÷ĄķÓÉ£»
¢Śµ±GĪŖCFÖŠµć£¬Į¬½ÓGE£¬ČōAB=![]() £¬ĒóĻ߶ĪGEµÄ³¤£®
£¬ĒóĻ߶ĪGEµÄ³¤£®
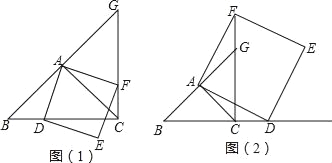
”¾“š°ø”æ(1) BC=CG£¬BC”ĶCG (2) ¢ŁČŌČ»³ÉĮ¢ ¢Ś![]()
”¾½āĪö”æ·ÖĪö£ŗ£Ø1£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻACB=”ĻABC=45”ć£¬ÓÉÕż·½ŠĪµÄŠŌÖŹµĆµ½AD=AF£¬”ĻDAF=90”ć£¬ÓɽĒµÄŗĶ²īµĆµ½”ĻBAD=”ĻCAF£¬ĶĘ³ö”÷BAD”Õ”÷CAF£ØSAS£©£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻACF=”ĻB=45”ć£¬BD=CF£¬Ö¤µĆBC”ĶCG£¬Ķ¬Ąķ”÷ADC”Õ”÷AFG£¬¼“æɵƵ½½įĀŪ£»
£Ø2£©¢Łøł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻACB=”ĻABC=45”ć£¬ÓÉÕż·½ŠĪµÄŠŌÖŹµĆµ½AD=AF£¬”ĻDAF=90”ć£¬ÓɽĒµÄŗĶ²īµĆµ½”ĻBAD=”ĻCAF£¬ĶĘ³ö”÷BAD”Õ”÷CAF£ØSAS£©£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻACF=”ĻB=45”ć£¬BD=CF£¬Ö¤µĆBC”ĶCG£¬Ķ¬Ąķ”÷ADC”Õ”÷AFG£¬¼“æɵƵ½½įĀŪ£»¢ŚÓė¢ŁĶ¬Ąķ£¬æɵĆBD=CF£¬BC=CG£¬BC”ĶCG£¬øł¾ŻŅŃÖŖĢõ¼žµĆµ½BC=CG=FG=CD=2£¬ČēĶ¼£Ø2£©£¬¹żµćA×÷AM”ĶBDÓŚM£¬øł¾Ż¹“¹É¶ØĄķµĆµ½AD=![]() £¬¹żµćE×÷EN”ĶFGÓŚN£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½FG=AM=1£¬ĶĘ³öNEĪŖFGµÄ“¹Ö±Ę½·ÖĻߣ¬¼“æɵƵ½½įĀŪ£®
£¬¹żµćE×÷EN”ĶFGÓŚN£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹµĆµ½FG=AM=1£¬ĶĘ³öNEĪŖFGµÄ“¹Ö±Ę½·ÖĻߣ¬¼“æɵƵ½½įĀŪ£®
Ļź½ā£ŗ£Ø1£©BC=CG£¬BC”ĶCG£®
”ß”ĻBAC=90”ć£¬AB=AC£¬”ą”ĻACB=”ĻABC=45”ć£®
”ßĖıߊĪADEFŹĒÕż·½ŠĪ£¬”ąAD=AF£¬”ĻDAF=90”ć£®
”ß”ĻBAD=90”ć©”ĻDAC£¬”ĻCAF=90”ć©”ĻDAC£¬”ą”ĻBAD=”ĻCAF£¬ŌņŌŚ”÷BADŗĶ”÷CAFÖŠ£¬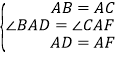 £¬”ą”÷BAD”Õ”÷CAF£ØSAS£©£¬”ą”ĻACF=”ĻB=45”ć£¬BD=CF£¬”ą”ĻBCF=”ĻACB+”ĻACF=90”ć£¬”ąBC”ĶCG£¬Ķ¬Ąķ”÷ADC”Õ”÷AFG£¬”ąCD=GF£¬”ąBD+CD=CF+GF£¬¼“BC=CG£®
£¬”ą”÷BAD”Õ”÷CAF£ØSAS£©£¬”ą”ĻACF=”ĻB=45”ć£¬BD=CF£¬”ą”ĻBCF=”ĻACB+”ĻACF=90”ć£¬”ąBC”ĶCG£¬Ķ¬Ąķ”÷ADC”Õ”÷AFG£¬”ąCD=GF£¬”ąBD+CD=CF+GF£¬¼“BC=CG£®
¹Ź“š°øĪŖ£ŗBC=CG£¬BC”ĶCG£»
£Ø2£©¢ŁČŌČ»³ÉĮ¢
”ßĖıߊĪADEFŹĒÕż·½ŠĪ£¬”ąAD=AF£¬”ĻDAF=90”ć£®
”ß”ĻBAD=90”ć©”ĻDAC£¬”ĻCAF=90”ć©”ĻDAC£¬”ą”ĻBAD=”ĻCAF£¬ŌņŌŚ”÷BADŗĶ”÷CAFÖŠ£¬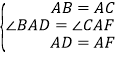 £¬”ą”÷BAD”Õ”÷CAF£ØSAS£©£¬”ą”ĻACF=”ĻB=45”ć£¬BD=CF£¬”ą”ĻBCF=”ĻACB+”ĻACF=90”ć£¬”ąBC”ĶCG£¬Ķ¬Ąķ”÷ADC”Õ”÷AFG£¬”ąCD=GF£¬”ąBD+CD=CF+GF£¬¼“BC=CG£»
£¬”ą”÷BAD”Õ”÷CAF£ØSAS£©£¬”ą”ĻACF=”ĻB=45”ć£¬BD=CF£¬”ą”ĻBCF=”ĻACB+”ĻACF=90”ć£¬”ąBC”ĶCG£¬Ķ¬Ąķ”÷ADC”Õ”÷AFG£¬”ąCD=GF£¬”ąBD+CD=CF+GF£¬¼“BC=CG£»
¢ŚÓė¢ŁĶ¬Ąķ£¬æɵĆBD=CF£¬BC=CG£¬BC”ĶCG£®
”ßAB=![]() £¬GĪŖCFÖŠµć£¬”ąBC=CG=FG=CD=2£¬ČēĶ¼£Ø2£©£¬¹żµćA×÷AM”ĶBDÓŚM£¬”ąAM=1£¬MD=3£¬”ąAD=
£¬GĪŖCFÖŠµć£¬”ąBC=CG=FG=CD=2£¬ČēĶ¼£Ø2£©£¬¹żµćA×÷AM”ĶBDÓŚM£¬”ąAM=1£¬MD=3£¬”ąAD=![]() £¬¹żµćE×÷EN”ĶFGÓŚN£®ŌŚ”÷AMDÓė”÷FNEÖŠ£¬
£¬¹żµćE×÷EN”ĶFGÓŚN£®ŌŚ”÷AMDÓė”÷FNEÖŠ£¬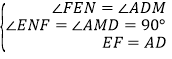 £¬”ą”÷AMD”Õ”÷FNE£¬”ąFN=AM=1£¬”ąFG=2FN£¬”ąNEĪŖFGµÄ“¹Ö±Ę½·ÖĻߣ¬¼“GE=FE=AD=
£¬”ą”÷AMD”Õ”÷FNE£¬”ąFN=AM=1£¬”ąFG=2FN£¬”ąNEĪŖFGµÄ“¹Ö±Ę½·ÖĻߣ¬¼“GE=FE=AD=![]() £®
£®


 æŚĖćĢāæر±¾©ø¾Å®¶łĶƳö°ęÉēĻµĮŠ“š°ø
æŚĖćĢāæر±¾©ø¾Å®¶łĶƳö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ŅŃÖŖ£¬ČēĶ¼£¬µćDŹĒ”÷ABCµÄ±ßABµÄÖŠµć£¬ĖıߊĪBCEDŹĒĘ½ŠŠĖıߊĪ£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪADCEŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ŌŚ”÷ABCÖŠ£¬ČōAC£½BC£¬ŌņĖıߊĪADCEŹĒ”” ””£»£ØÖ»Š“½įĀŪ£¬²»ŠčÖ¤Ć÷£©
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±AC”ĶBCŹ±£¬ĒóÖ¤£ŗĖıߊĪADCEŹĒÕż·½ŠĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ”÷ABC£¬·Ö±šŅŌBC£¬AB£¬ACĪŖ±ß×÷µČ±ßČż½ĒŠĪBCE£¬ACF£¬ABD
(1)Čō“ęŌŚĖıߊĪADEF£¬ÅŠ¶ĻĖüµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
(2)“ęŌŚĖıߊĪADEFµÄĢõ¼žĻĀ£¬ĒėÄćøų”÷ABCĢķøöĢõ¼ž£¬Ź¹µĆĖıߊĪADEF³ÉĪŖ¾ŲŠĪ£¬²¢ĖµĆ÷ĄķÓÉ£®
(3)µ±”÷ABCĀś×ćŹ²Ć“Ģõ¼žŹ±ĖıߊĪADEF²»“ęŌŚ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĮŠø÷Ź½£ŗ
![]() =
=![]() -1£»
-1£»
![]() £»
£»
![]() .
.
£Ø1£©øł¾ŻĒ°Ćęø÷Ź½µÄ¹ęĀÉæÉµĆ£ŗ
¢Ł![]() .
.
¢Ś![]() .
.
£Ø2£©ĒėÓĆÉĻĆęµÄ½įĀŪ½ųŠŠ¼ĘĖć£ŗ
¢Ł![]() £Ø“š°øæÉŗ¬ÓŠĆŻµÄŠĪŹ½±ķŹ¾£©£»
£Ø“š°øæÉŗ¬ÓŠĆŻµÄŠĪŹ½±ķŹ¾£©£»
¢ŚČō![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒÅ×ĪļĻߊĪ¹°ĒÅ£¬µ±¹°¶„ĄėĖ®Ćę2mŹ±£¬Ė®Ćęæķ4m£¬ŌņĖ®ĆęĻĀ½µ1mŹ±£¬Ė®Ćęæķ¶ČŌö¼Ó_____m£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,”÷ABCÖŠ,”ĻBAC=75”ć,BC=7,”÷ABCµÄĆ껿ĪŖ14,DĪŖ BC±ßÉĻŅ»¶Æµć(²»ÓėB,CÖŲŗĻ)£¬½«”÷ABDŗĶ”÷ACD·Ö±šŃŲÖ±ĻßAB£¬AC·ÕŪµĆµ½”÷ABEÓė”÷ACF£¬ÄĒĆ“”÷AEFµÄĆ껿×īŠ”ÖµĪŖ___.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćB”¢CŌŚĻ߶ĪADµÄŅģ²ą£¬µćE”¢F·Ö±šŹĒĻ߶ĪAB”¢CDÉĻµÄµć£®ŅŃÖŖ”ĻAEG£½”ĻAGE£¬”ĻDCG£½”ĻDGC.

(1) ĒóÖ¤£ŗAB”ĪCD
(2) Čō”ĻAGE£«”ĻAHF£½180”ć£¬ĒŅ”ĻBFC£30”ć£½2”ĻC£¬Ēó”ĻBµÄ¶ČŹż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»¶łĶÆ·ž×°ÉĢµźŌŚĻśŹŪÖŠ·¢ĻÖ£ŗÄ³Ę·ÅĘĶÆ×°Ę½¾łĆæĢģæÉŹŪ³ö20¼ž£¬Ć漞ÓÆĄū40ŌŖ.ĪŖĮĖÓ½Ó”°Įł”¤Ņ»”±¶łĶƽŚ£¬ÉĢµź¾ö¶Ø²ÉČ”ŹŹµ±µÄ½µ¼Ū“ėŹ©£¬Ą©“óĻśŹŪĮ棬Ōö¼ÓÓÆĄū£¬¾”æģ¼õÉŁæā“ę.¾ŹŠ³”µ÷²é·¢ĻÖ£ŗČē¹ūĆ漞ĶÆ×°½µ¼Ū1ŌŖ£¬ÄĒĆ“Ę½¾łĆæĢģ¾ĶæɶąŹŪ³ö2¼ž.ŅŖĻėĘ½¾łĆæĢģĻśŹŪÕāÖÖĶÆ×°ÉĻÓÆĄū1200ŌŖ£¬ÄĒĆ“Ć漞ĶÆ×°Ó¦½µ¼Ū¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”õABCDÖŠ£¬BEĘ½·Ö”ĻABC½»ADÓŚµćE£¬DFĘ½·Ö”ĻADC½»BCÓŚµćF£®
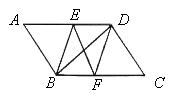
”¾1”æ”÷ABE”Õ”÷CDF
”¾2”æČōBD”ĶEF£¬ŌņÅŠ¶ĻĖıߊĪEBFDŹĒŹ²Ć“ĢŲŹāĖıߊĪ£¬ĒėÖ¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com