
【题目】某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳绳 | 25 | a |
实心球 | 20 |
|
50m | b | 0.4 |
拔河 | 0.15 |
(1)直接写出a= ,b= ;
(2)将图中的扇形统计图补充完整(注明项目、百分比);
(3)若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?

【答案】(1)0.25、40;(2)见解析(3)660
【解析】试题分析:(1)首先根据跳绳的频率是a=25%=0.25,有25人,据此即可求得总人数,然后利用除以总人数即可求得b的值;
(2)用360°乘以各自的频率即可求出圆心角,即可解答;
(3)用总人数1200乘以喜爱50m和拔河的学生频率即可求解.
试题解析:(1)由扇形图知a=25%=0.25,
∵总人数为25÷0.25=100(人),
∴b=100×0.4=40,
故答案为:0.25、40;
(2)如图,
实心球所占百分比为![]()
50m所占百分比为0.4=40%,拔河所占百分比为0.15=15%,
补全扇形图如下:

(3)1200×(0.4+0.15)=660(人),
答:全校共有学生1200名,估计该校最喜爱50m和拔河的学生的学生大约有660人.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
科目:初中数学 来源: 题型:
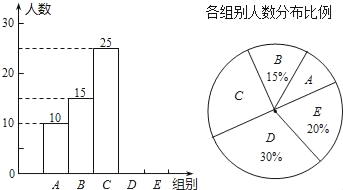
【题目】重庆八中宏帆中学某年级为了选拔参加“全国汉字听写大赛”重庆赛区比赛的队员,特在年级举行全体学生的“汉字听写”比赛,首轮每位学生听写汉字39个.现随机抽取了部分学生的听写结果,绘制成如图的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)已知该年级共有1500名学生,如果听写正确的字的个数不少于24个则进入第二轮的比赛,请你估计本次听写比赛顺利进入第二轮的学生人数;
(3)第二轮比赛过后,为了更有针对性地应对本次大赛,该年级决定从没有担任班主任的5个语文老师(其中3个男老师2个女老师)中随机抽取两个老师对胜出的学生进行培训、辅导.请用树状图或列表法求出抽取的两个老师恰好都是男老师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放置的是一副斜边相等的直角三角板,其中AB=BC,连接BD交公共的斜边AC于O点.
(1)证明:BD平分∠ADC;
(2)求∠COD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=![]()
B. BC=1,AC=2,AB=![]()
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,点D、E分别为边BC、AC上的点,连接DE,过点E作EF∥BC交AB于F,若BC=CE,CD=6,AE=8,∠EDB=2∠A,则BC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销水杯,电热水壶两种商品,水杯每个进价15元,售价20元;电热水壶每个进价35元,售价45元.
(1)若该商场同时购进水杯、电热水壶共100件,恰好用去2700元,求能购进水杯、电热水壶各多少个?
(2)商场要求小明用1050元的钱(必须全部用完)采购水杯、电热水壶(或其中一种商品),且还要求总利润不少于340元(假设商品全部卖完),请你确定所有的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com