
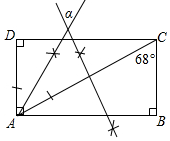
 如图,依据尺规作图的痕迹,计算∠α=56°.
如图,依据尺规作图的痕迹,计算∠α=56°. 分析 先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=$\frac{1}{2}$∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°-34°=56°,
∴∠α=56°.
故答案为:56.
点评 本题考查的是作图-基本作图,熟知角平分线及线段垂直平分线的作法是解答此题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
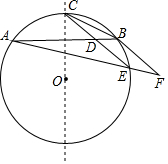 如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 两点之间线段最短 | |
| B. | 两点确定一条直线 | |
| C. | 垂线段最短 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.
某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
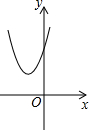 已知二次函数y=(x+m)2-n的图象如图所示,则一次函数y=mx+n与反比例函数y=$\frac{mn}{x}$的图象可能是( )
已知二次函数y=(x+m)2-n的图象如图所示,则一次函数y=mx+n与反比例函数y=$\frac{mn}{x}$的图象可能是( )| A. | 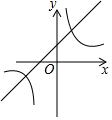 | B. | 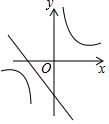 | C. | 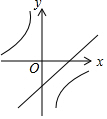 | D. | 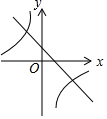 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查孝感区居民对创建“全国卫生城市”的知晓度,宜采用抽样调查 | |
| B. | 一组数据85,95,90,95,95,90,90,80,95,90的众数为95 | |
| C. | “打开电视,正在播放乒乓球比赛”是必然事件 | |
| D. | 同时抛掷两枚质地均匀的硬币一次,出现两个正面朝上的概率为$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
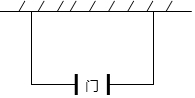 如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.
如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.| A. | 15 | B. | 16 | C. | 18 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com