
【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
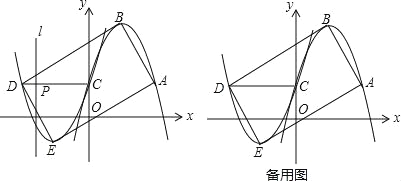
【答案】(1)A(2,1)、C(0,1)、D(﹣2,1);(2)a=﹣![]() ,y2=
,y2=![]() x2+2
x2+2![]() x+1;(3)S=
x+1;(3)S=![]() t2(0≤t≤1)或S=﹣
t2(0≤t≤1)或S=﹣![]()
![]() (1<t≤2).
(1<t≤2).
【解析】
试题分析:(1)直接将点A的坐标代入y1=ax2﹣2ax+1得出m的值,因为由图象可知点A在第一象限,所以m≠0,则m=2,写出A,C的坐标,点D与点A关于点C对称,由此写出点D的坐标;
(2)根据顶点坐标公式得出抛物线y1的顶点B的坐标,再由矩形对角线相等且平分得:BC=CD,在直角△BMC中,由勾股定理列方程求出a的值得出抛物线y1的解析式,由旋转的性质得出抛物线y2的解析式;
(3)分两种情况讨论:①当0≤t≤1时,S=S△GHD=S△PDH+S△PDG,作辅助线构建直角三角形,求出PG和PH,利用面积公式计算;②当1<t≤2时,S=S直角三角形+S矩形﹣S不重合,这里不重合的图形就是△GE′F,利用30°角和60°角的直角三角形的性质进行计算得出结论.
试题解析:(1)由题意得:
将A(m,1)代入y1=ax2﹣2ax+1得:am2﹣2am+1=1,
解得:m1=2,m2=0(舍),
∴A(2,1)、C(0,1)、D(﹣2,1);
(2)如图1,由(1)知:B(1,1﹣a),过点B作BM⊥y轴,
若四边形ABDE为矩形,则BC=CD,
∴BM2+CM2=BC2=CD2,
∴12+(﹣a)2=22,
∴a=![]() ,
,
∵y1抛物线开口向下,
∴a=﹣![]() ,
,
∵y2由y1绕点C旋转180°得到,则顶点E(﹣1,1﹣![]() ),
),
∴设y2=a(x+1)2+1﹣![]() ,则a=
,则a=![]() ,
,
∴y2=![]() x2+2
x2+2![]() x+1;
x+1;
(3)如图1,当0≤t≤1时,则DP=t,构建直角△BQD,
得BQ=![]() ,DQ=3,则BD=2
,DQ=3,则BD=2![]() ,
,
∴∠BDQ=30°,
∴PH=![]() ,PG=
,PG=![]() t,
t,
∴S=![]() (PE+PF)×DP=
(PE+PF)×DP=![]() t2,
t2,
如图2,当1<t≤2时,EG=E′G=![]() (t﹣1),E′F=2(t﹣1),
(t﹣1),E′F=2(t﹣1),
S不重合=![]() (t﹣1)2,
(t﹣1)2,
S=S1+S2﹣S不重合=![]() +
+![]() (t﹣1)﹣
(t﹣1)﹣![]() (t﹣1)2,
(t﹣1)2,
=﹣![]()
![]() ;
;
综上所述:S=![]() t2(0≤t≤1)或S=﹣
t2(0≤t≤1)或S=﹣![]()
![]() (1<t≤2).
(1<t≤2).



科目:初中数学 来源: 题型:
【题目】若a2+2ab=﹣10,b2+2ab=16,则多项式a2+4ab+b2与a2﹣b2的值分别为( )
A. 6,26 B. ﹣6,26 C. 6,﹣26 D. ﹣6,﹣26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABD、△BCE、△ACF都是等边三角形。

(1)试判断四边形ADEF的形状并说明理由.
(2)当△ABC满足_____,四边形ADEF是矩形(不需证明).
(3)当△ABC满足____,四边形ADEF是菱形(不需证明).
(4)当△ABC满足 ,四边形ADEF不存在. (不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水库的平均水位为80米,在此基础上,若水位变化时,把水位上升记为正数;水库管理员记录了3月~8月水位变化的情况(单位:米):-5,-4,0,+3,+6,+8.试问这几个月的实际水位是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若P(m,n)与Q(n,m)表示同一个点,那么这个点一定在( )
A. 第二、四象限 B. 第一、三象限 C. 平行于x轴的直线上 D. 平行于y轴的直线上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com