证明:(1)由题意,得y+b=k(x+1),
整理,得y=kx+(k-b),
∵k≠0,k-b与k均为常数,
∴y是x的一次函数;
(2)由(1)知y=kx+(k-b),
∵点P(b,k)与点Q(1,-

)关于原点对称,
∴
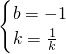
,
解之,得b=-1,k=±1,
∵一次函数随x的增大而增大,
∴k>0,k=-1舍去,
从而知b=-1,k=1,
则一次函数的解析式为y=x+2.
分析:(1)根据y+b与x+1成正比例,设出解析式,整理得到y为x的一次函数;
(2)由P与Q关于原点对称求出b与k的值,代入(1)求出的一次函数解析式中,根据一次函数随x的增大而增大,得到k大于0,确定出k与b的值,即可确定出一次函数解析式.
点评:此题考查了待定系数法求一次函数解析式,一次函数的定义,以及关于原点对称点的特点,熟练掌握待定系数法是解本题的关键.

 )关于原点对称,求这个一次函数的解析式.
)关于原点对称,求这个一次函数的解析式. )关于原点对称,
)关于原点对称,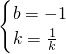 ,
,
