
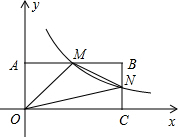
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,反比例函数y=$\frac{k}{x}$的图象经过点M,N,若M是AB的中点,△OMN的面积为3.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,反比例函数y=$\frac{k}{x}$的图象经过点M,N,若M是AB的中点,△OMN的面积为3.分析 (1)设B点坐标为(a,b),根据中点坐标公式可得M($\frac{1}{2}$a,b),由反比例函数图象上点的坐标特征得到N(a,$\frac{1}{2}$b).根据△OMN的面积为3,列出方程ab-$\frac{1}{2}$•a•$\frac{1}{2}$b-$\frac{1}{2}$•$\frac{1}{2}$a•b-$\frac{1}{2}$•$\frac{1}{2}$a•$\frac{1}{2}$b=3,求得ab=8,那么k=$\frac{1}{2}$ab=4,进而得到反比例函数的解析式;
(2)将点M($\frac{1}{2}$a,b)代入y=-$\frac{1}{2}$x+3,得到b=-$\frac{1}{2}$×$\frac{1}{2}$a+3,即a=12-4b,代入ab=8,得出(12-4b)b=8,解方程求出b的值,进而得到点B的坐标.
解答 解:(1)设B点坐标为(a,b),
∵M是AB的中点,
∴M($\frac{1}{2}$a,b),
∵反比例函数y=$\frac{k}{x}$的图象经过点M,N,
∴N(a,$\frac{1}{2}$b).
∵△OMN的面积为3,
∴ab-$\frac{1}{2}$•a•$\frac{1}{2}$b-$\frac{1}{2}$•$\frac{1}{2}$a•b-$\frac{1}{2}$•$\frac{1}{2}$a•$\frac{1}{2}$b=3,
∴ab=8,
∴k=$\frac{1}{2}$ab=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
(2)∵点M($\frac{1}{2}$a,b)在直线y=-$\frac{1}{2}$x+3上,
∴b=-$\frac{1}{2}$×$\frac{1}{2}$a+3,即a=12-4b,
又∵ab=8,
∴(12-4b)b=8,
解得b=1或2,
当b=1时,a=8,点B的坐标为(8,1);
当b=2时,a=4,点B的坐标为(4,2).
综上所述,点B的坐标为(8,1)或(4,2).
点评 本题考查了反比例函数与一次函数图象的交点问题,中点坐标公式,反比例函数、一次函数图象上点的坐标特征,三角形的面积,待定系数法求反比例函数的解析式,一元二次方程的解法,难度中等.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形ABCD的边长为6cm,点E在AE上,AE=2cm,动点F由点C开始以3cm/s的速度沿折线CBE移动,动点G同时由点D开始以1cm/s沿点DC移动2.5秒后以点D、G、F、E为顶点的四边形是平行四边形.
正方形ABCD的边长为6cm,点E在AE上,AE=2cm,动点F由点C开始以3cm/s的速度沿折线CBE移动,动点G同时由点D开始以1cm/s沿点DC移动2.5秒后以点D、G、F、E为顶点的四边形是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com