
【题目】如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD向点D运动;点Q从点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达点D时,点Q也停止运动,连接BP,过点P作BP的垂线交过点Q平行于CD的直线l于点E,BE于CD相交于点F,连接PF,设点P运动时间为t(s),
(1)求∠PBE的度数;
(2)当t为何值时,△PQF是以PF为腰的等腰三角形?
(3)试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.

【答案】(1)证明见解析(2)t=2s或4s时,△PFQ是以PF为腰的等腰三角形(3)△PDF的周长是定值
【解析】试题分析:(1)如图1中,只要证明△ABP≌△QPE,推出PB=PE即可求解.
(2)如图2中,分两种情形讨论①当AP=PD时,可以推出△PFQ是等腰三角形,此时t=2.
②当点P与点D重合时,PF=CD=AD=DQ,△PFQ是等腰三角形,此时t=4.
(3)如图3中,△PDF的周长是定值.将△BCF绕点B顺时针旋转90°得到△BAG,只要证明△PBG≌△PBF,推出PF=PG,推出PF=PA+AG=PA+CF,由此即可证明.
试题解析:
(1)如图1中,
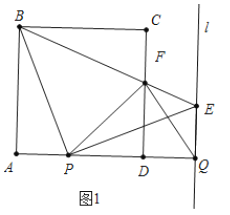
∵四边形ABCD是正方形,
∴AB=AD,∠A=90°,
∵AP=DQ,
∴AD=PQ=AB,
∵PB⊥PE,
∴∠BPE=90°,
∴∠ABP+∠APB=90°,∠APB+∠EPQ=90°,
∴∠ABP=∠EPQ,
∴△ABP≌△QPE,
∴PB=PE,
∴∠PBE=∠PEB=45°.
(2)如图2中,
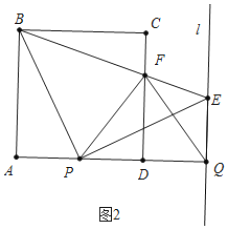
①当AP=PD时,
∵AP=DQ,
∴DP=DQ,
∵FD⊥PQ,
∴PF=FQ,
∴△PFQ是等腰三角形,此时t=2.
②当点P与点D重合时,PF=CD=AD=DQ,△PFQ是等腰三角形,此时t=4.
综上所述,t=2s或4s时,△PFQ是以PF为腰的等腰三角形.
(3)如图3中,△PDF的周长是定值.
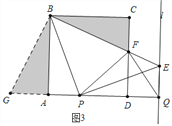
将△BCF绕点B顺时针旋转90°得到△BAG.
∵∠PBE=45°,∠ABC=90°,
∴∠ABP+∠CBF=∠ABP+∠ABG=45°,
∴∠PBG=∠PBF,
在△PBG和△PBF中,
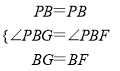 ,
,
∴△PBG≌△PBF,
∴PF=PG,
∴PF=PA+AG=PA+CF,
∴△PDF的周长=PF+DP+DF=(PA+DP)+(DF+CF)=AD+CD=8.
∴△PDF的周长为定值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究: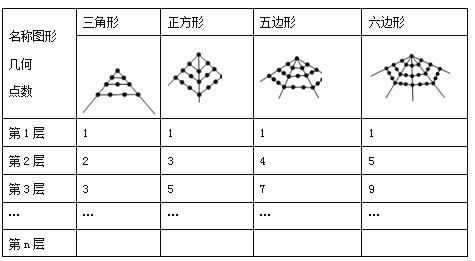
(1)六边形第5层的几何点数是 ;第n层的几何点数是 .
(2)在第 层时,六边形的几何点数是三角形的几何点数的3.5倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(k+1)x+![]() k2+1=0有两个实数根.
k2+1=0有两个实数根.
(1)求k的取值范围;
(2)若抛物线y=x2﹣(k+1)x+![]() k2+1与x轴交于A、B两点,点A、点B到原点O的距离分别为OA、OB,且满足OA+OB﹣4OAOB+5=0,求k的值.
k2+1与x轴交于A、B两点,点A、点B到原点O的距离分别为OA、OB,且满足OA+OB﹣4OAOB+5=0,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于点A(﹣1,0),B(3,0)、C(0,﹣3)三点.
(1)直接写出抛物线的解析式 ;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD,试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由.
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′,在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒(0≤t≤3),试求S与t之间的函数关系式?
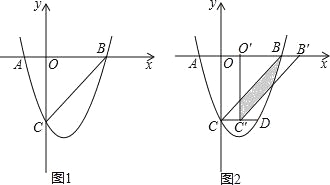
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年实现生产总值达280亿的目标,用科学记数法表示“280亿”为( )
A. 28×109 B. 2.8×108 C. 2.8×109 D. 2.8×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林城市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
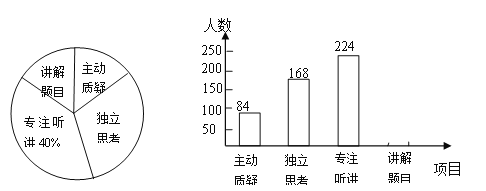
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动,电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动,则第2017次相遇在( ) 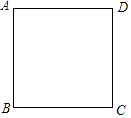
A.点 A
B.点B
C.点C
D.点D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com