
分析 当点E在BC上,在AB上截取AG=EC,连接GE,如图1,通过证明△AEG≌△EFC得到AE=EF;当E点在BC的延长线上时,延长BA到G,使AG=CE,连接GE,如图2,通过证明△MAE≌△CEF得到AE=EF;如图3,当AM=BE时,易得△ADM≌△BAE,则DM=AE,DM⊥AE,所以DM=EF,DM∥EF,于是可判断四边形MEFD是平行四边形;如图4,当AE⊥AC时,易得AEFC为矩形,加上AE=EF,则可判断四边形AEFC为正方形;由于AE⊥EF,则NE不能垂直EF,于是可判断在边AB上不存在点N,使得NEFD是矩形.
解答 解:当点E在BC上,在AB上截取AG=EC,连接GE,如图1,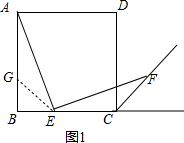
∵四边形ABCD为正方形,
∴AB=BC,∠B=∠BCD=90°,
∵AE⊥EF,
∴∠AEB+∠CEF=90°,
而∠AEB+∠BAE=90°,
∴∠BAE=∠CEF,
∵AG=EC,AB=BC,
∴BG=BE,
∴∠BGE=45°,
而F在∠BCD的外角平分线上,
∴∠AGE=∠ECF=135°,
在△AEM和△EFC中,
$\left\{\begin{array}{l}{∠EAG=∠FEC}\\{AG=EC}\\{∠AGE=∠ECF}\end{array}\right.$,
∴△AEG≌△EFC(ASA),
∴AE=EF;
当E点在BC的延长线上时,延长BA到G,使AG=CE,连接GE, 如图2,
如图2,
∴BG=BE,
∴∠BGE=45°,
∴∠BGE=∠ECF,
又∵AD∥BE,
∴∠DAE=∠BEA,
又∵∠GAD=∠AEF=90°,
∴∠DAE+∠GAD=∠BEA+∠AEF,
即∠GAE=∠CEF,
在△GAE和△CEF中,
$\left\{\begin{array}{l}{∠G=∠ECF}\\{AG=CE}\\{∠GAE=∠CEF}\end{array}\right.$,
∴△MAE≌△CEF(ASA),
∴AE=EF,所以①正确;
如图3,当AM=BE时,易得△ADM≌△BAE,
∴DM=AE,DM⊥AE,
∵AE⊥EF,AE=EF,
∴DM=EF,DM∥EF,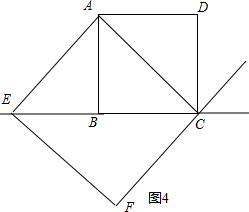
∴四边形MEFD是平行四边形,所以②正确;
如图4,当AE⊥AC时,易得AEFC为矩形,
而AE=EF,
∴四边形AEFC为正方形,所以③正确;
∵AE⊥EF,
∴NE不能垂直EF,
∴在边AB上不存在点N,使得NEFD是矩形,所以④错误.
故答案为①②③.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了正方形的判定与性质、三角形全等的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.
如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=$-\frac{3}{4}x+3$与直线y=$kx-\frac{16}{3}$交于x轴上的同一个点A,直线y=$-\frac{3}{4}x+3$与y轴交于点B,直线y=$kx-\frac{16}{3}$与y轴的交点为C.
已知直线y=$-\frac{3}{4}x+3$与直线y=$kx-\frac{16}{3}$交于x轴上的同一个点A,直线y=$-\frac{3}{4}x+3$与y轴交于点B,直线y=$kx-\frac{16}{3}$与y轴的交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
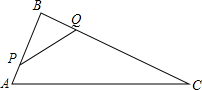 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com