
分析 先求出方程组的即,得出不等式组,求出不等式组的整数解,即可得出答案.
解答 解:$\left\{\begin{array}{l}{3x+4y=m①}\\{4x+3y=5②}\end{array}\right.$
①×4-②×3得:y=$\frac{4m-15}{7}$,
①×3-②×4得:x=$\frac{20-3m}{7}$,
当$\left\{\begin{array}{l}{x=\frac{20-3m}{7}≥0}\\{y=\frac{4m-15}{7}≥0}\end{array}\right.$,
此不等式组的解集为$\frac{15}{4}$≤m≤$\frac{20}{3}$,
整数m=4或5或6,
即存在这样的整数m,使方程组$\left\{\begin{array}{l}{3x+4y=m}\\{4x+3y=5}\end{array}\right.$的解是一对非负数,
当m=4时,方程组的解是$\left\{\begin{array}{l}{x=\frac{8}{7}}\\{y=\frac{1}{7}}\end{array}\right.$;
当m=5时,方程组的解是$\left\{\begin{array}{l}{x=\frac{5}{7}}\\{y=\frac{5}{7}}\end{array}\right.$;
当m=6时,方程组的解是$\left\{\begin{array}{l}{x=\frac{2}{7}}\\{y=\frac{9}{7}}\end{array}\right.$.
点评 本题考查了解二元一次方程组,解一元一次不等式组,不等式组的整数解等知识点,能得出关于m的不等式组是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
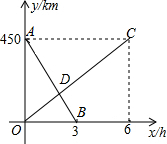 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示,慢车离乙地的路程y2(km)与行驶的时间x(h) 之间的函数关系,如图中线段OC所示,根据图象进行以下探究.
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示,慢车离乙地的路程y2(km)与行驶的时间x(h) 之间的函数关系,如图中线段OC所示,根据图象进行以下探究.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a,b在数轴上的位置如图所示,则下面关系式中正确的个数是( )
有理数a,b在数轴上的位置如图所示,则下面关系式中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
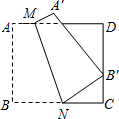 如图,四边形ABCD是边长为8的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=4.
如图,四边形ABCD是边长为8的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
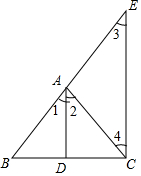 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com