
Ϊ����ʵ����Ժ��ָʾ����ij�ط�������̨��һϵ�С���ũ���Ż����ߣ�ʹũ�������������ӣ�ijũ����������һ��ũ��Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊÿǧ��20Ԫ���г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ������¹�ϵ��y=��2x+80�������ֲ�Ʒÿ�����������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ��
��2���ò�Ʒ���ۼ۶�Ϊÿǧ�˶���Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲�����ÿǧ��28Ԫ����ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊÿǧ�˶���Ԫ��
��1��w=-2x2+120x-1600����2��30��200����3��25.
���������������1���������۶�=�����������۵��ۣ��г�������ϵʽ��
��2�����䷽������2���ĺ�����ϵʽ���Σ����ö��κ��������������ֵ��
��3����y=150���루2���ĺ�����ϵʽ�У���һԪ���η�����x������x��ȡֵ��Χ��x��ֵ��
�����������1���������w=��x-20��?y=��x-20����-2x+80��=-2x2+120x-1600��
��w��x�ĺ�����ϵʽΪ��w=-2x2+120x-1600��
��2��w=-2x2+120x-1600=-2��x-30��2+200��
��-2��0��
�൱x=30ʱ��w�����ֵ��w���ֵΪ200��
�𣺸ò�Ʒ���ۼ۶�Ϊÿǧ��30Ԫʱ��ÿ������������������������200Ԫ��
��3����w=150ʱ���ɵ÷���-2��x-30��2+200=150��
��� x1=25��x2=35��
��35��28��
��x2=35���������⣬Ӧ��ȥ��
�𣺸�ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊÿǧ��25Ԫ��
����: ���κ�����Ӧ�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪:���κ���y=x2-4x+3.
��1����y=x2-4x+3���� ����ʽ��
����ʽ��
��2������ö��κ���ͼ��ĶԳ���Ͷ������ꣻ
��3����xȡ��ֵʱ��y��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���
��1����֤������aΪ��ʵ�����˺���ͼ����x�������������㣮
��2����a<0�����˺���ͼ����x�����������ľ���Ϊ ʱ������˶��κ����Ľ���ʽ��
ʱ������˶��κ����Ľ���ʽ��
��3���ڣ�2���������£����˶��κ���ͼ����x�ύ��A��B���㣬�ں���ͼ�����Ƿ���ڵ�P��ʹ�á�PAB�����Ϊ �����������P�����꣬����������˵�����ɡ�
�����������P�����꣬����������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��˾Ͷ���½���һ�̳�����������30�䣮��Ԥ�⣬��ÿ��������Ϊ10��Ԫʱ����ȫ�������ÿ��������ÿ����5000Ԫ�����������1�䣮���������������Ӷ��Ϊ5000Ԫ�����������ù�˾ҪΪ���������ÿ��ÿ�꽻���ַ���2��Ԫ��δ���������ÿ��ÿ�꽻���ַ���1��Ԫ��
��1����ÿ�����̵������Ϊ12��Ԫʱ����������ټ䣿�����������Ԫ��
��2����ÿ�����̵������Ϊ������Ԫʱ���ù�˾��������������ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ���y=kx+n��ͼ����x���y��ֱ��ڵ�A��6��0����B��0�� �����߶�AB�Ĵ�ֱƽ���߽�x���ڵ�C����AB�ڵ�D.
�����߶�AB�Ĵ�ֱƽ���߽�x���ڵ�C����AB�ڵ�D.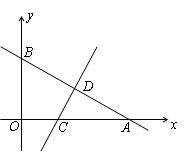
��1����ȷ�����һ�κ�������ʽ����3�֣�
��2�����A��B��C����������ߵĺ�����ϵʽ����6�֣�
��3�������������������ߵ�ͼ��ش𣺵�xȡ��ֵʱ���������еIJ���ͼ������x����Ϸ��� ��3�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ڹ���x��y�Ķ�Ԫһ�η����� �У�
�У�
��1����a=3������Ľ⣻
��2����S=a��3x+y������aΪ��ֵʱ��S����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������� ��
�� ���ཻ�ڵ�
���ཻ�ڵ� ����1��0����
����1��0���� ��3��0������
��3��0������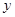 ���ཻ�ڵ�
���ཻ�ڵ� ����
���� Ϊ�߶�
Ϊ�߶� �ϵĶ��㣨����
�ϵĶ��㣨���� ��
�� �غϣ�������
�غϣ������� ��ֱ��
��ֱ�� ���ֱ�����������߶�
���ֱ�����������߶� �ֱ��ڵ�
�ֱ��ڵ� ��
�� ����
���� ��
��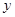 ���������ϣ�
���������ϣ� =2������
=2������ ��
�� ��
��
��1���������ߵĽ���ʽ��
��2�����ı��� ��ƽ���ı���ʱ�����
��ƽ���ı���ʱ����� �����ꣻ
�����ꣻ
��3������ ��ֱ�߽���2���е�ƽ���ı���
��ֱ�߽���2���е�ƽ���ı��� �ֳ������ȵ������֣�������ֱ�ߵĽ���ʽ��������˵��ƽ��ƽ���ı�����������ɣ�
�ֳ������ȵ������֣�������ֱ�ߵĽ���ʽ��������˵��ƽ��ƽ���ı�����������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������ �Ǻ���
�Ǻ���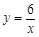 �ڵ�һ�����ڵ�ͼ���������Ǻ���
�ڵ�һ�����ڵ�ͼ���������Ǻ��� ��ͼ��
��ͼ�� ��
�� ��������
�������� �ϣ���
�ϣ��� ����������
����������
��1��������еĵ� ��
��
��2���� ����ȡ������ֱ�ߣ������в�ֱͬ�ߵ�������
����ȡ������ֱ�ߣ������в�ֱͬ�ߵ�������
��3���ӣ�2��������ֱ������ȡһ��ֱ�ߣ�����ȡֱ�����������й�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ �У�A��BΪx�������㣬C��DΪy���ϵ����㣬��
�У�A��BΪx�������㣬C��DΪy���ϵ����㣬��
����A��C��B�������ߵ�һ����C1�뾭����A��D��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�������
�����߳�Ϊ�����ߡ�����֪��C������Ϊ��0�� ������M��������C2��
������M��������C2�� ��
�� ��0���Ķ��㣮
��0���Ķ��㣮
��1����A��B��������ꣻ
��2�������ߡ��ڵ����������Ƿ����һ��P��ʹ�á�PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
��3������BDMΪֱ��������ʱ���� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com