
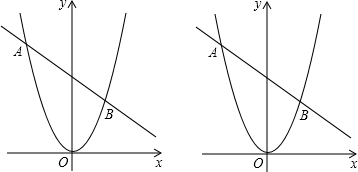
分析 (1)要求定点的坐标,只需寻找一个合适x,使得y的值与k无关即可.
(2)只需联立两函数的解析式,就可求出点A、B的坐标.设出点P的横坐标为a,运用割补法用a的代数式表示△APB的面积,然后根据条件建立关于a的方程,从而求出a的值,进而求出点P的坐标
(3)联立直线与抛物线解析式,整理可得到关于x的一元二次方程,由题意可知该方程有两个相等的实数根,其判别式为零,可得到关于k的方程,可求得k的值.
解答 解:(1)∵当x=-2时,y=(-2)k+2k+4=4.
∴直线AB:y=kx+2k+4必经过定点(-2,4).
∴点C的坐标为(-2,4).
(2)∵k=-$\frac{1}{2}$,
∴直线的解析式为y=-$\frac{1}{2}$x+3.
联立$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=\frac{1}{2}{x}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-3}\\{y=\frac{9}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
∴点A的坐标为(-3,$\frac{9}{2}$),点B的坐标为(2,2).
过点P作PQ∥y轴,交AB于点Q,
过点A作AM⊥PQ,垂足为M,
过点B作BN⊥PQ,垂足为N,如图1所示.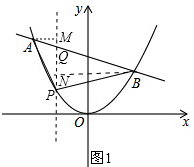
设点P的横坐标为a,则点Q的横坐标为a.
∴yP=$\frac{1}{2}$a2,yQ=-$\frac{1}{2}$a+3.
∵点P在直线AB下方,
∴PQ=yQ-yP
=-$\frac{1}{2}$a+3-$\frac{1}{2}$a2
∵AM+NB=a-(-3)+2-a=5.
∴S△APB=S△APQ+S△BPQ
=$\frac{1}{2}$PQ•AM+$\frac{1}{2}$PQ•BN
=$\frac{1}{2}$PQ•(AM+BN)
=$\frac{1}{2}$(-$\frac{1}{2}$a+3-$\frac{1}{2}$a2)•5
=5.
整理得:a2+a-2=0.
解得:a1=-2,a2=1.
当a=-2时,yP=$\frac{1}{2}$×(-2)2=2.
此时点P的坐标为(-2,2).
当a=1时,yP=$\frac{1}{2}$×12=$\frac{1}{2}$.
此时点P的坐标为(1,$\frac{1}{2}$).
∴符合要求的点P的坐标为(-2,2)或(1,$\frac{1}{2}$).
(3)由$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}}\\{y=kx+2k+1}\end{array}\right.$消去y得到x2-2kx-4k-2=0,
∵直线AB与抛物线y=$\frac{1}{2}$x2只有一个交点,
∴△=0,
∴4k2+16k+8=0,
∴k2+4k+2=0,
∴k=-2±$\sqrt{2}$.
点评 本题考查了解方程组、解一元二次方程、一元二次方程根与系数的关系、勾股定理、相似三角形的性质与判定等知识,考查了通过解方程组求两函数交点坐标、用割补法表示三角形的面积等方法,综合性比较强.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一正方形桌面ABCD,一顶点B在水平地面上,其中两顶点A、C到地面的距离分别是0.5m和1m,则桌面的边长为$\frac{1}{2}$$\sqrt{5}$m.
如图,有一正方形桌面ABCD,一顶点B在水平地面上,其中两顶点A、C到地面的距离分别是0.5m和1m,则桌面的边长为$\frac{1}{2}$$\sqrt{5}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
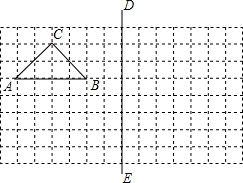 如图,在所给网格图(每小格均为边长是1的正方形)中完成下各题:(用直尺画图)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下各题:(用直尺画图)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com