
【题目】如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF =45°,则∠ABC的度数为( )
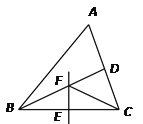
A. 45° B. 50° C. 55° D. 60°
【答案】B
【解析】 设∠ABD=∠CBD=x°,则∠ABC=2x°,根据线段垂直平分线性质求出BF=CF,推出∠FCB=∠CBD,根据三角形内角和定理得出方程,求出方程的解即可.
解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
设∠ABD=∠CBD=x°,则∠ABC=2x°,
∵EF是BC的垂直平分线,
∴BF=CF,
∴∠FCB=∠CBD=x°,
∵∠A=60°,∠ACF=45°,
∴60°+45°+x°+2x°=180°,
解得:x=25,
∴∠ABC=2x°=50°,
故选B.
“点睛”本题考查了三角形内角和定理,线段垂直平分线性质的应用,能求出BF=CF是解此题的关键,注意线段垂直平分线上的点到线段两个端点的距离相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外)。
(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把10a2(x+y)2-5a(x+y)3因式分解时,应提取的公因式是( )
A.5a B.(x+y)2 C.5(x+y)2 D.5a(x+y)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣1向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
A.y=(x+2)2+1
B.y=(x﹣2)2﹣1
C.y=(x﹣2)2+1
D.y=(x+2)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
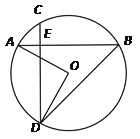
【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点随之停止运动.(设运动时间为t秒) 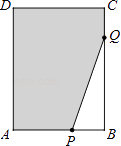
(1)如果存在某一时刻恰好使QB=2PB,求出此时t的值;
(2)在(1)的条件下,求图中阴影部分的面积(结果保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com